设计自适应实验来研究工作记忆

在大多数机器学习中，我们从数据开始，然后学习模型。在其他情况下，我们也可以参与数据生成过程。这给了我们一个令人兴奋的机会：我们可以尝试获取有助于模型更有效学习的数据。这个过程被称为最优实验设计 (OED)，Pyro 通过 pyro.contrib.oed 模块支持选择最优设计。

使用 OED 时，数据生成和建模过程如下

1. 写下一个贝叶斯模型，其中包含一个设计参数、一个未知隐变量和一个可观测变量。

2. 选择最优设计（稍后详述）。

3. 收集数据并拟合模型，例如使用 SVI。

我们还可以进行多轮或多次实验迭代。这样做时，我们将从步骤 3 中学到的模型用作下一轮步骤 1 中的先验。这种方法特别有用，因为它允许我们根据已经学到的东西来设计下一个实验：实验是自适应的。

在本教程中，我们将通过一个具体的例子来展示多轮 OED 的整个过程。我们将展示如何设计自适应实验来学习参与者的工作记忆容量。我们将要自适应的设计是要求参与者记住的数字序列的长度。让我们深入了解完整的细节。

实验设置

假设你，作为参与者，被展示一个数字序列

\[1\ 4\ 7\ 0\ 9\]

然后将其隐藏。你必须凭记忆准确地重现这个序列。在下一轮中，序列的长度可能会不同

\[6\ 5\ 0\ 2\ 8\ 0 .\]

你能记住的最长序列就是你的工作记忆容量。在本教程中，我们建立一个工作记忆的贝叶斯模型，并用它来运行一系列自适应实验，从而非常快速地学习某人的工作记忆容量。

工作记忆模型

我们为上述数字实验的单轮建立的模型包含三个组成部分：参与者需要记住的序列长度 \(l\)，参与者的真实工作记忆容量 \(\theta\)，以及实验结果 \(y\)，表示他们是否成功记住序列（\(y=1\)）或未能记住（\(y=0\)）。我们根据（臭名昭著的）“神奇的数字七，加减二”[1]选择工作记忆容量的先验。

注意：\(\theta\) 实际上代表了参与者正确记住序列的概率为 50/50 的那个点。

import torch

import pyro
import pyro.distributions as dist


sensitivity = 1.0
prior_mean = torch.tensor(7.0)
prior_sd = torch.tensor(2.0)


def model(l):
    # Dimension -1 of `l` represents the number of rounds
    # Other dimensions are batch dimensions: we indicate this with a plate_stack
    with pyro.plate_stack("plate", l.shape[:-1]):
        theta = pyro.sample("theta", dist.Normal(prior_mean, prior_sd))
        # Share theta across the number of rounds of the experiment
        # This represents repeatedly testing the same participant
        theta = theta.unsqueeze(-1)
        # This define a *logistic regression* model for y
        logit_p = sensitivity * (theta - l)
        # The event shape represents responses from the same participant
        y = pyro.sample("y", dist.Bernoulli(logits=logit_p).to_event(1))
        return y

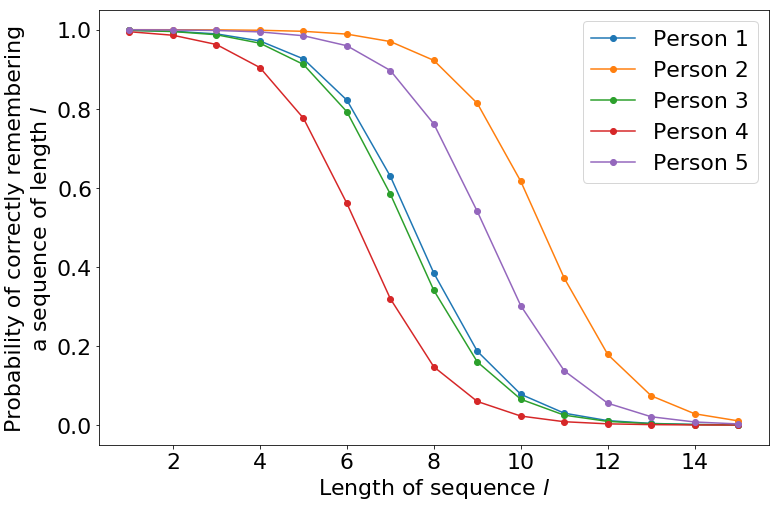
成功记住序列的概率如下所示，针对 \(\theta\) 的五个随机样本进行了绘制。

import matplotlib
import matplotlib.pyplot as plt

matplotlib.rcParams.update({'font.size': 22})

# We sample five times from the prior
theta = (prior_mean + prior_sd * torch.randn((5,1)))
l = torch.arange(1, 16, dtype=torch.float)
# This is the same as using 'logits=' in the prior above
prob = torch.sigmoid(sensitivity * (theta - l))

plt.figure(figsize=(12, 8))
for curve in torch.unbind(prob, 0):
    plt.plot(l.numpy(), curve.numpy(), marker='o')
plt.xlabel("Length of sequence $l$")
plt.ylabel("Probability of correctly remembering\na sequence of length $l$")
plt.legend(["Person {}".format(i+1) for i in range(5)])
plt.show()

模型推断

有了这个模型，我们快速演示一下 Pyro 中对这个模型的变分推断。我们定义一个 Normal 引导（guide）用于变分推断。

from torch.distributions.constraints import positive

def guide(l):
    # The guide is initialised at the prior
    posterior_mean = pyro.param("posterior_mean", prior_mean.clone())
    posterior_sd = pyro.param("posterior_sd", prior_sd.clone(), constraint=positive)
    pyro.sample("theta", dist.Normal(posterior_mean, posterior_sd))

最后，我们指定以下数据：参与者被展示了长度为 5、7 和 9 的序列。他们正确记住了前两个，但没有记住第三个。

l_data = torch.tensor([5., 7., 9.])
y_data = torch.tensor([1., 1., 0.])

现在我们可以对模型运行 SVI。

from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam

conditioned_model = pyro.condition(model, {"y": y_data})
svi = SVI(conditioned_model,
          guide,
          Adam({"lr": .001}),
          loss=Trace_ELBO(),
          num_samples=100)
pyro.clear_param_store()
num_iters = 5000
for i in range(num_iters):
    elbo = svi.step(l_data)
    if i % 500 == 0:
        print("Neg ELBO:", elbo)

Neg ELBO: 1.6167092323303223
Neg ELBO: 3.706324815750122
Neg ELBO: 0.9958380460739136
Neg ELBO: 1.0630500316619873
Neg ELBO: 1.1738307476043701
Neg ELBO: 1.6654635667800903
Neg ELBO: 1.296904444694519
Neg ELBO: 1.305729627609253
Neg ELBO: 1.2626266479492188
Neg ELBO: 1.3095542192459106

print("Prior:     N({:.3f}, {:.3f})".format(prior_mean, prior_sd))
print("Posterior: N({:.3f}, {:.3f})".format(pyro.param("posterior_mean"),
                                            pyro.param("posterior_sd")))

Prior:     N(7.000, 2.000)
Posterior: N(7.749, 1.282)

在我们的后验分布下，我们可以看到我们对参与者工作记忆容量有了更新的估计，并且我们的不确定性现在降低了。

贝叶斯最优实验设计

到目前为止都很标准。在前面的例子中，长度 l_data 的选择并没有经过深思熟虑。幸运的是，在这种情况下，可以使用更复杂的策略来选择序列长度，以充分利用我们提出的每个问题。

我们使用贝叶斯最优实验设计 (BOED) 来做到这一点。在 BOED 中，我们感兴趣的是设计能够最大化信息增益的实验，其正式定义为

\[\text{IG}(l, y) = KL(p(\theta|y,l)||p(\theta)) .\]

其中 \(KL\) 代表 Kullback-Leiber 散度。

换句话说，信息增益是后验分布与先验分布之间的 KL 散度。因此，它代表了我们通过运行长度为 \(l\) 的实验并获得结果 \(y\) 来“移动”后验分布的距离。

不幸的是，在实际运行实验之前，我们无法知道 \(y\)。因此，我们基于预期信息增益 [2] 来选择 \(l\)

\[\text{EIG}(l) = \mathbb{E}_{y\sim p(y|\theta,l)} [KL(p(\theta|y,l)||p(\theta))].\]

由于它包含后验密度 \(p(y|\theta,l)\)，EIG 并不直接可计算。然而，我们可以利用以下 EIG 的变分估计器 [3]

\[\text{EIG}(l) = \min_q \mathbb{E}_{\theta,y \sim p(\theta)p(y|\theta,l)} \left[ \log \frac{p(y|\theta,l)}{q(y|l)} \right].\]

Pyro 中的最优实验设计

幸运的是，Pyro 提供了估算 EIG 的现成工具。我们只需在上面的公式中定义“边际引导”（marginal guide）\(q(y|l)\)。

def marginal_guide(design, observation_labels, target_labels):
    # This shape allows us to learn a different parameter for each candidate design l
    q_logit = pyro.param("q_logit", torch.zeros(design.shape[-2:]))
    pyro.sample("y", dist.Bernoulli(logits=q_logit).to_event(1))

这不像在 Pyro 中通常遇到并用于 SVI 的那些引导用于推断。相反，这种引导只采样观测到的采样点：在本例中是 "y"。这是有道理的，因为传统引导近似后验分布 \(p(\theta|y, l)\)，而我们的引导近似边际分布 \(p(y|l)\)。

from pyro.contrib.oed.eig import marginal_eig

# The shape of `candidate_designs` is (number designs, 1)
# This represents a batch of candidate designs, each design is for one round of experiment
candidate_designs = torch.arange(1, 15, dtype=torch.float).unsqueeze(-1)
pyro.clear_param_store()
num_steps, start_lr, end_lr = 1000, 0.1, 0.001
optimizer = pyro.optim.ExponentialLR({'optimizer': torch.optim.Adam,
                                      'optim_args': {'lr': start_lr},
                                      'gamma': (end_lr / start_lr) ** (1 / num_steps)})

eig = marginal_eig(model,
                   candidate_designs,       # design, or in this case, tensor of possible designs
                   "y",                     # site label of observations, could be a list
                   "theta",                 # site label of 'targets' (latent variables), could also be list
                   num_samples=100,         # number of samples to draw per step in the expectation
                   num_steps=num_steps,     # number of gradient steps
                   guide=marginal_guide,    # guide q(y)
                   optim=optimizer,         # optimizer with learning rate decay
                   final_num_samples=10000  # at the last step, we draw more samples
                                            # for a more accurate EIG estimate
                  )

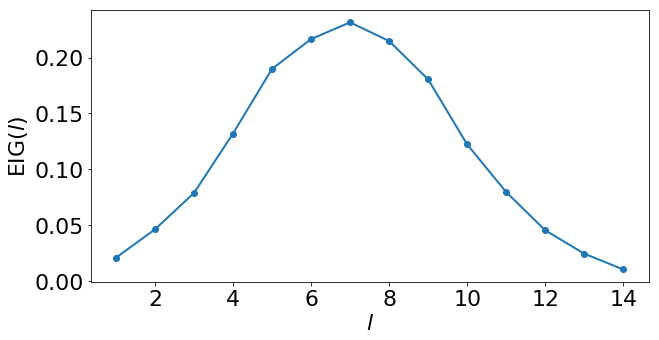
我们可以将找到的 EIG 估计值可视化。

plt.figure(figsize=(10,5))
matplotlib.rcParams.update({'font.size': 22})
plt.plot(candidate_designs.numpy(), eig.detach().numpy(), marker='o', linewidth=2)
plt.xlabel("$l$")
plt.ylabel("EIG($l$)")
plt.show()

best_l = 1 + torch.argmax(eig)
print("Optimal design:", best_l.item())

Optimal design: 7

这告诉我们第一轮实验应该使用长度为 7 的序列。请注意，虽然我们可能凭直觉猜到这个最优设计，但同样的框架同样适用于更复杂的模型和实验，在这些场景中凭直觉找到最优设计更具挑战性。

作为训练的附带结果，我们的边际引导 \(q(y|l)\) 近似地学习了边际分布 \(p(y|l)\)。

q_prob = torch.sigmoid(pyro.param("q_logit"))
print("   l | q(y = 1 | l)")
for (l, q) in zip(candidate_designs, q_prob):
    print("{:>4} | {}".format(int(l.item()), q.item()))

   l | q(y = 1 | l)
   1 | 0.9849993586540222
   2 | 0.9676634669303894
   3 | 0.9329487681388855
   4 | 0.871809720993042
   5 | 0.7761920690536499
   6 | 0.6436398029327393
   7 | 0.4999988079071045
   8 | 0.34875917434692383
   9 | 0.22899287939071655
  10 | 0.13036076724529266
  11 | 0.06722454726696014
  12 | 0.03191758319735527
  13 | 0.015132307074964046
  14 | 0.00795808993279934

这个拟合张量的元素代表了对于 candidate_designs 中每个可能的序列长度 \(l\) 对应的 \(y\) 的边际分布。我们已经对未知变量 \(\theta\) 进行了边缘化，因此这个拟合张量显示的是“平均”参与者的概率。

自适应实验

现在我们有了构建自适应实验来研究工作记忆的要素。我们重复以下步骤

1. 使用 EIG 找到最优序列长度 \(l\)

2. 使用长度为 \(l\) 的序列进行测试

3. 用新数据更新后验分布

在第一次迭代中，步骤 1 使用上述先验。然而，对于后续迭代，我们使用基于所有现有数据的后验。

在本 notebook 中，“实验”使用以下合成器进行

def synthetic_person(l):
    # The synthetic person can remember any sequence shorter than 6
    # They cannot remember any sequence of length 6 or above
    # (There is no randomness in their responses)
    y = (l < 6.).float()
    return y

以下代码允许我们在收集更多数据时更新模型。

def make_model(mean, sd):
    def model(l):
        # Dimension -1 of `l` represents the number of rounds
        # Other dimensions are batch dimensions: we indicate this with a plate_stack
        with pyro.plate_stack("plate", l.shape[:-1]):
            theta = pyro.sample("theta", dist.Normal(mean, sd))
            # Share theta across the number of rounds of the experiment
            # This represents repeatedly testing the same participant
            theta = theta.unsqueeze(-1)
            # This define a *logistic regression* model for y
            logit_p = sensitivity * (theta - l)
            # The event shape represents responses from the same participant
            y = pyro.sample("y", dist.Bernoulli(logits=logit_p).to_event(1))
            return y
    return model

现在我们准备好了，可以运行一个使用自适应设计的 10 步实验。

ys = torch.tensor([])
ls = torch.tensor([])
history = [(prior_mean, prior_sd)]
pyro.clear_param_store()
current_model = make_model(prior_mean, prior_sd)

for experiment in range(10):
    print("Round", experiment + 1)

    # Step 1: compute the optimal length
    optimizer = pyro.optim.ExponentialLR({'optimizer': torch.optim.Adam,
                                          'optim_args': {'lr': start_lr},
                                          'gamma': (end_lr / start_lr) ** (1 / num_steps)})
    eig = marginal_eig(current_model, candidate_designs, "y", "theta", num_samples=100,
                       num_steps=num_steps, guide=marginal_guide, optim=optimizer,
                       final_num_samples=10000)
    best_l = 1 + torch.argmax(eig).float().detach()

    # Step 2: run the experiment, here using the synthetic person
    print("Asking the participant to remember a sequence of length", int(best_l.item()))
    y = synthetic_person(best_l)
    if y:
        print("Participant remembered correctly")
    else:
        print("Participant could not remember the sequence")
    # Store the sequence length and outcome
    ls = torch.cat([ls, best_l.expand(1)], dim=0)
    ys = torch.cat([ys, y.expand(1)])

    # Step 3: learn the posterior using all data seen so far
    conditioned_model = pyro.condition(model, {"y": ys})
    svi = SVI(conditioned_model,
              guide,
              Adam({"lr": .005}),
              loss=Trace_ELBO(),
              num_samples=100)
    num_iters = 2000
    for i in range(num_iters):
        elbo = svi.step(ls)

    history.append((pyro.param("posterior_mean").detach().clone().numpy(),
                    pyro.param("posterior_sd").detach().clone().numpy()))
    current_model = make_model(pyro.param("posterior_mean").detach().clone(),
                               pyro.param("posterior_sd").detach().clone())
    print("Estimate of \u03b8: {:.3f} \u00b1 {:.3f}\n".format(*history[-1]))

Round 1
Asking the participant to remember a sequence of length 7
Participant could not remember the sequence
Estimate of θ: 5.788 ± 1.636

Round 2
Asking the participant to remember a sequence of length 6
Participant could not remember the sequence
Estimate of θ: 4.943 ± 1.252

Round 3
Asking the participant to remember a sequence of length 5
Participant remembered correctly
Estimate of θ: 5.731 ± 1.043

Round 4
Asking the participant to remember a sequence of length 6
Participant could not remember the sequence
Estimate of θ: 5.261 ± 0.928

Round 5
Asking the participant to remember a sequence of length 5
Participant remembered correctly
Estimate of θ: 5.615 ± 0.859

Round 6
Asking the participant to remember a sequence of length 6
Participant could not remember the sequence
Estimate of θ: 5.423 ± 0.888

Round 7
Asking the participant to remember a sequence of length 6
Participant could not remember the sequence
Estimate of θ: 5.092 ± 0.763

Round 8
Asking the participant to remember a sequence of length 5
Participant remembered correctly
Estimate of θ: 5.371 ± 0.717

Round 9
Asking the participant to remember a sequence of length 5
Participant remembered correctly
Estimate of θ: 5.597 ± 0.720

Round 10
Asking the participant to remember a sequence of length 6
Participant could not remember the sequence
Estimate of θ: 5.434 ± 0.640

现在我们可视化 \((\theta)\) 的后验分布演变

import numpy as np
from scipy.stats import norm
import matplotlib.colors as colors
import matplotlib.cm as cmx


matplotlib.rcParams.update({'font.size': 22})
cmap = plt.get_cmap('winter')
cNorm  = colors.Normalize(vmin=0, vmax=len(history)-1)
scalarMap = cmx.ScalarMappable(norm=cNorm, cmap=cmap)
plt.figure(figsize=(12, 6))
x = np.linspace(0, 14, 100)
for idx, (mean, sd) in enumerate(history):
    color = scalarMap.to_rgba(idx)
    y = norm.pdf(x, mean, sd)
    plt.plot(x, y, color=color)
    plt.xlabel("$\\theta$")
    plt.ylabel("p.d.f.")
plt.show()

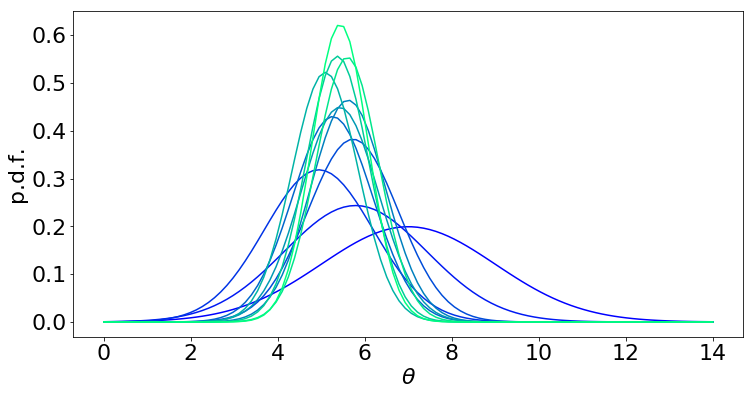
（蓝色 = 先验，浅绿色 = 10 步后验）

相比之下，假设我们使用一种简单的设计：尝试长度为 1, 2, …, 10 的序列。

pyro.clear_param_store()
ls = torch.arange(1, 11, dtype=torch.float)
ys = synthetic_person(ls)
conditioned_model = pyro.condition(model, {"y": ys})
svi = SVI(conditioned_model,
          guide,
          Adam({"lr": .005}),
          loss=Trace_ELBO(),
          num_samples=100)
num_iters = 2000
for i in range(num_iters):
    elbo = svi.step(ls)

plt.figure(figsize=(12,6))
matplotlib.rcParams.update({'font.size': 22})
y1 = norm.pdf(x, pyro.param("posterior_mean").detach().numpy(),
              pyro.param("posterior_sd").detach().numpy())
y2 = norm.pdf(x, history[-1][0], history[-1][1])
plt.plot(x, y1)
plt.plot(x, y2)
plt.legend(["Simple design", "Optimal design"])
plt.xlabel("$\\theta$")
plt.ylabel("p.d.f.")
plt.show()

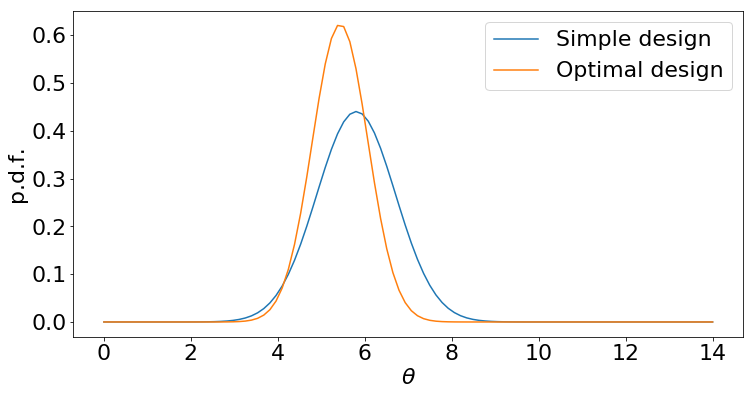
尽管两种设计策略都能提供数据，但最优策略最终得到的后验分布更尖锐：这意味着我们对最终答案更有信心，或者可以更早停止实验。

扩展

在本教程中，我们使用变分推断来拟合 \(\theta\) 的近似后验。这可以用其他后验推断策略代替，例如哈密顿蒙特卡洛（Hamiltonian Monte Carlo）。

本教程中的模型非常简单，可以通过多种方式进行扩展。例如，除了衡量参与者是否记住了序列，我们还可能收集其他信息。我们可以建立一个模型来预测犯错的数量（例如，正确序列与参与者回应之间的编辑距离），或者联合建模正确性和响应时间。这里有一个示例模型，我们使用 LogNormal 分布来模拟响应时间，如 [4] 所示。

time_intercept = 0.5
time_scale = 0.5

def model(l):
    theta = pyro.sample("theta", dist.Normal(prior_mean, prior_sd))
    logit_p = sensitivity * (theta - l)
    correct = pyro.sample("correct", dist.Bernoulli(logits=logit_p))
    mean_log_time = time_intercept + time_scale * (theta - l)
    time = pyro.sample("time", dist.LogNormal(mean_log_time, 1.0))
    return correct, time

仍然可以使用 marginal_eig 计算 EIG。我们会将 "y" 替换为 ["correct", "time"]，并且边际引导现在将对 "correct" 和 "time" 这两个点的联合分布进行建模。

我们的模型还做了一些假设，我们可以选择放宽这些假设。例如，我们假设所有相同长度的序列都同样容易记住。我们还将 sensitivity 固定为一个已知常数：我们可能需要学习这个值。我们还可以考虑在两个层面上进行学习：学习用于群体趋势的全局变量，以及用于个体效应的局部变量。当前模型只是一个针对个体的模型。在这些场景下，EIG 仍然可以作为选择最优设计的手段。

参考文献

[1] Miller, G.A., 1956. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological review, 63(2), p.81.

[2] Chaloner, K. and Verdinelli, I., 1995. Bayesian experimental design: A review. Statistical Science, pp.273-304.

[3] Foster, A., Jankowiak, M., Bingham, E., Horsfall, P., Teh, Y.W., Rainforth, T. and Goodman, N., 2019. Variational Bayesian Optimal Experimental Design. Advances in Neural Information Processing Systems 2019 (to appear).

[4] van der Linden, W.J., 2006. A lognormal model for response times on test items. Journal of Educational and Behavioral Statistics, 31(2), pp.181-204.