变分自编码器¶

简介¶

变分自编码器（VAE）可以说是实现深度概率建模的最简单设置。请注意，我们在此处选择措辞时非常谨慎。VAE 本身并不是一个模型——更确切地说，VAE 是用于对特定类别的模型进行变分推断的一种特殊设置。这类模型的范围非常广泛：基本上包括任何带有潜随机变量的（无监督）密度估计器。这类模型的基本结构很简单，甚至简单得令人惊讶（见图 1）。

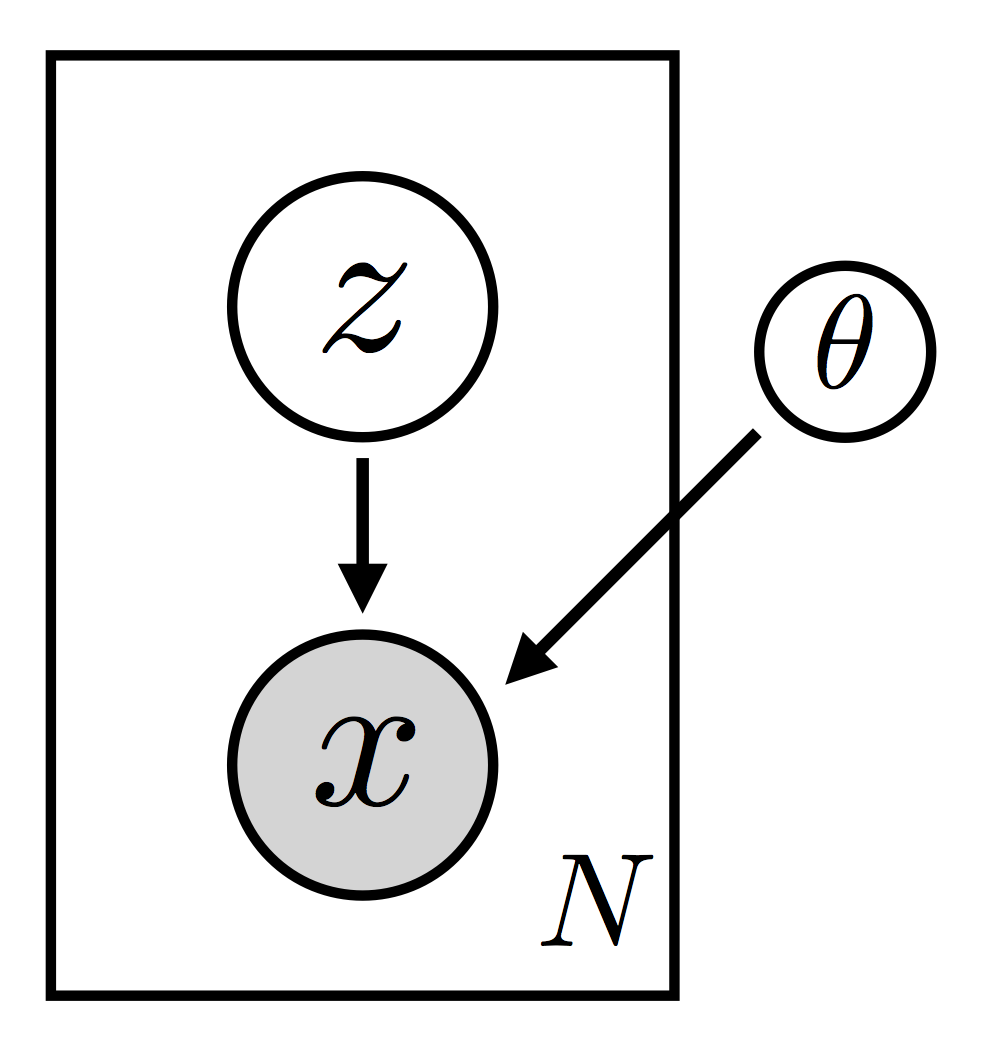
这里我们将我们感兴趣的模型结构描绘成一个图模型。我们有 \(N\) 个观测数据点 \(\{ \bf x_i \}\)。每个数据点由一个（局部）潜随机变量 \(\bf z_i\) 生成。还有一个参数 \(\theta\)，它之所以是全局的，是因为所有数据点都依赖于它（这也是为什么它被画在矩形外面）。注意，由于 \(\theta\) 是一个参数，我们不对它进行贝叶斯处理。最后，这里特别重要的是，我们允许每个 \(\bf x_i\) 以复杂、非线性的方式依赖于 \(\bf z_i\)。在实践中，这种依赖关系将由一个带有参数 \(\theta\) 的（深度）神经网络参数化。正是这种非线性使得对这类模型的推断特别具有挑战性。

当然，这种非线性结构也是这类模型为复杂数据建模提供非常灵活方法的原因之一。确实值得强调的是，模型的每个组件都可以以各种不同的方式“重新配置”。例如

\(p_\theta({\bf x} | {\bf z})\) 中的神经网络可以按照所有常规方式进行变化（层数、非线性类型、隐藏单元数等）
我们可以选择适合当前数据集的观测似然：高斯分布、伯努利分布、范畴分布等。
我们可以选择潜在空间的维度数量

图模型表示是思考模型结构的一种有用方式，但查看联合概率密度的显式因式分解也可能富有成效

\[p({\bf x}, {\bf z}) = \prod_{i=1}^N p_\theta({\bf x}_i | {\bf z}_i) p({\bf z}_i)\]

这样一个事实，即 \(p({\bf x}, {\bf z})\) 分解成这样的项的乘积，清楚地说明了我们将 \(\bf z_i\) 称为局部随机变量的含义。对于任何特定的 \(i\)，只有单个数据点 \(\bf x_i\) 依赖于 \(\bf z_i\)。因此，\(\{ \bf z_i\}\) 描述了局部结构，即每个数据点私有的结构。这种因式分解的结构也意味着我们可以在学习过程中进行子采样。因此，这类模型适用于大数据场景。（关于这方面和相关主题的更多讨论，请参阅 SVI 第二部分。）

模型就是这些了。由于观测值以复杂、非线性的方式依赖于潜随机变量，我们预计潜变量的后验分布具有复杂的结构。因此，为了在这种模型中进行推断，我们需要指定一系列灵活的引导函数（即变分分布）。由于我们希望能够扩展到大型数据集，我们的引导函数将利用分摊（amortization）来控制变分参数的数量（关于分摊的更一般讨论，请参阅 SVI 第二部分）。

回想一下，引导函数的作用是“猜测”潜随机变量的良好值——这里的“良好”是指它们既符合模型的先验分布，又符合数据。如果我们不使用分摊，我们将为每个数据点 \(\bf x_i\) 引入变分参数 \(\{ \lambda_i \}\)。这些变分参数将代表我们对 \(\bf z_i\) 的“良好”值的信念；例如，它们可以编码 \({\bf z}_i\) 空间中高斯分布的均值和方差。分摊意味着，我们不是引入变分参数 \(\{ \lambda_i \}\)，而是学习一个将每个 \(\bf x_i\) 映射到适当的 \(\lambda_i\) 的函数。由于我们需要这个函数具有灵活性，我们将其参数化为一个神经网络。因此，我们最终得到一个参数化的潜变量 \(\bf z\) 空间的分布族，可以针对所有 \(N\) 个数据点 \({\bf x}_i\) 进行实例化（见图 2）。

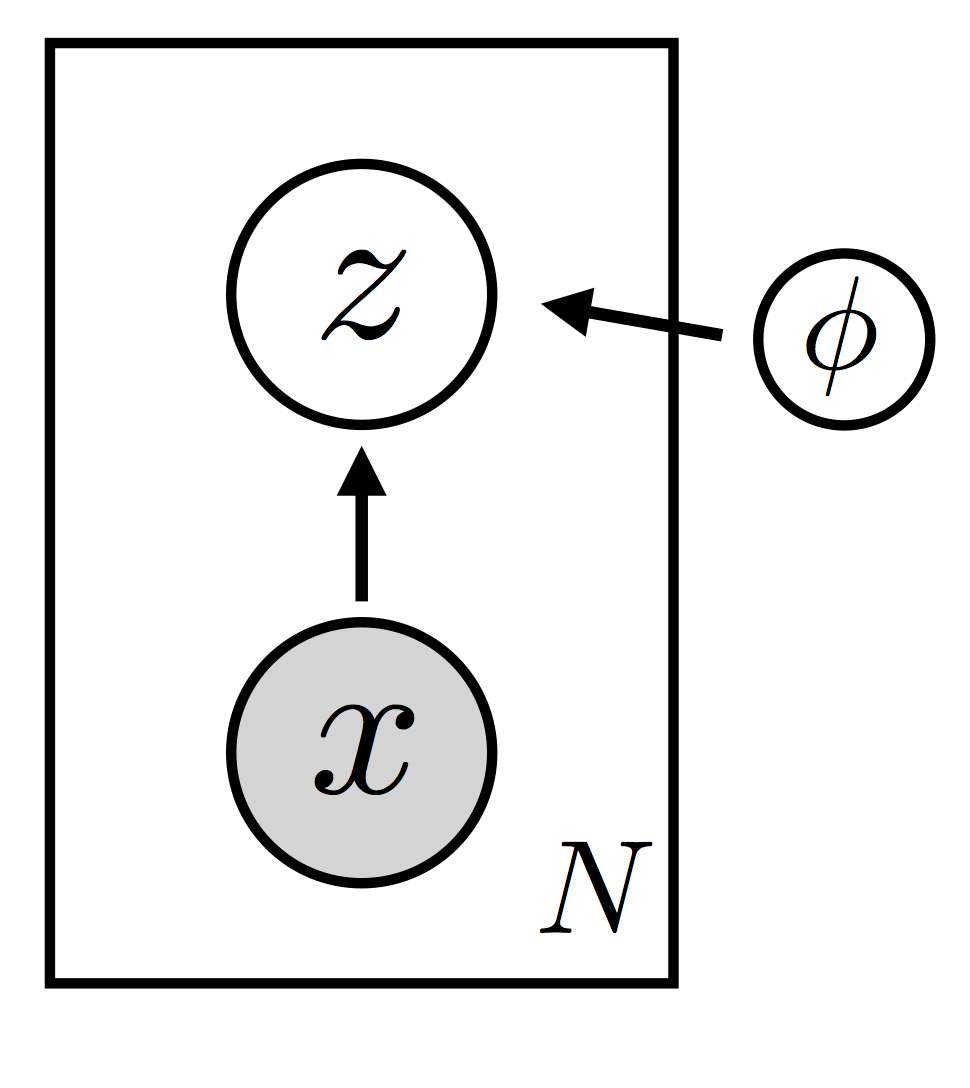
注意，引导函数 \(q_{\phi}({\bf z} | {\bf x})\) 由所有数据点共享的全局参数 \(\phi\) 参数化。推断的目标是找到 \(\theta\) 和 \(\phi\) 的“良好”值，以满足两个条件

对数证据 \(\log p_\theta({\bf x})\) 很大。这意味着我们的模型对数据拟合得很好
引导函数 \(q_{\phi}({\bf z} | {\bf x})\) 对后验分布提供了良好的近似

（关于随机变分推断的入门，请参阅 SVI 第一部分。）

此时，我们可以跳出细节，考虑我们设置的顶层结构。具体来说，假设 \(\{ \bf x_i \}\) 是图像，那么该模型就是一个图像的生成模型。一旦我们学习到 \(\theta\) 的良好值，我们就可以按如下方式从模型生成图像

根据先验分布 \(p({\bf z})\) 采样 \(\bf z\)
根据似然函数 \(p_\theta({\bf x}|{\bf z})\) 采样 \(\bf x\)

每张图像都由一个潜代码 \(\bf z\) 表示，该代码通过似然函数映射到图像，而似然函数取决于我们学到的 \(\theta\)。这就是为什么在这种情况下似然函数通常被称为解码器：它的作用是将 \(\bf z\) 解码成 \(\bf x\)。注意，由于这是一个概率模型，对于编码给定数据点 \(\bf x\) 的 \(\bf z\) 存在不确定性。

一旦我们学到了 \(\theta\) 和 \(\phi\) 的良好值，我们还可以进行以下练习。

我们从给定的图像 \(\bf x\) 开始
使用我们的引导函数将其编码为 \(\bf z\)
使用模型似然函数，我们解码 \(\bf z\) 并获得一个重建图像 \({\bf x}_{\rm reco}\)

如果我们学到了 \(\theta\) 和 \(\phi\) 的良好值，\(\bf x\) 和 \({\bf x}_{\rm reco}\) 应该相似。这应该能阐明“自编码器”这个词是如何最终被用来描述这种设置的：模型是解码器，引导函数是编码器。它们合在一起可以被视为一个自编码器。

Pyro 中的 VAE¶

让我们看看如何在 Pyro 中实现 VAE。我们要建模的数据集是 MNIST，这是一个手写数字图像的集合。由于这是一个流行的基准数据集，我们可以利用 PyTorch 便捷的数据加载器功能来减少需要编写的样板代码量

[ ]:

import os

import numpy as np
import torch
from pyro.contrib.examples.util import MNIST
import torch.nn as nn
import torchvision.transforms as transforms

import pyro
import pyro.distributions as dist
import pyro.contrib.examples.util  # patches torchvision
from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam

[ ]:

assert pyro.__version__.startswith('1.9.1')
pyro.distributions.enable_validation(False)
pyro.set_rng_seed(0)
# Enable smoke test - run the notebook cells on CI.
smoke_test = 'CI' in os.environ

[ ]:

# for loading and batching MNIST dataset
def setup_data_loaders(batch_size=128, use_cuda=False):
    root = './data'
    download = True
    trans = transforms.ToTensor()
    train_set = MNIST(root=root, train=True, transform=trans,
                      download=download)
    test_set = MNIST(root=root, train=False, transform=trans)

    kwargs = {'num_workers': 1, 'pin_memory': use_cuda}
    train_loader = torch.utils.data.DataLoader(dataset=train_set,
        batch_size=batch_size, shuffle=True, **kwargs)
    test_loader = torch.utils.data.DataLoader(dataset=test_set,
        batch_size=batch_size, shuffle=False, **kwargs)
    return train_loader, test_loader

这里需要强调的一点是，我们使用 transforms.ToTensor() 将像素强度归一化到范围 \([0.0, 1.0]\)。

接下来我们定义一个封装解码器网络的 PyTorch 模块

[ ]:

class Decoder(nn.Module):
    def __init__(self, z_dim, hidden_dim):
        super().__init__()
        # setup the two linear transformations used
        self.fc1 = nn.Linear(z_dim, hidden_dim)
        self.fc21 = nn.Linear(hidden_dim, 784)
        # setup the non-linearities
        self.softplus = nn.Softplus()
        self.sigmoid = nn.Sigmoid()

    def forward(self, z):
        # define the forward computation on the latent z
        # first compute the hidden units
        hidden = self.softplus(self.fc1(z))
        # return the parameter for the output Bernoulli
        # each is of size batch_size x 784
        loc_img = self.sigmoid(self.fc21(hidden))
        return loc_img

给定一个潜代码 \(z\)，Decoder 的前向调用返回图像空间中伯努利分布的参数。由于每张图像的大小是 \(28\times28=784\)，因此 loc_img 的大小是 batch_size x 784。

接下来我们定义一个封装编码器网络的 PyTorch 模块

[ ]:

class Encoder(nn.Module):
    def __init__(self, z_dim, hidden_dim):
        super().__init__()
        # setup the three linear transformations used
        self.fc1 = nn.Linear(784, hidden_dim)
        self.fc21 = nn.Linear(hidden_dim, z_dim)
        self.fc22 = nn.Linear(hidden_dim, z_dim)
        # setup the non-linearities
        self.softplus = nn.Softplus()

    def forward(self, x):
        # define the forward computation on the image x
        # first shape the mini-batch to have pixels in the rightmost dimension
        x = x.reshape(-1, 784)
        # then compute the hidden units
        hidden = self.softplus(self.fc1(x))
        # then return a mean vector and a (positive) square root covariance
        # each of size batch_size x z_dim
        z_loc = self.fc21(hidden)
        z_scale = torch.exp(self.fc22(hidden))
        return z_loc, z_scale

给定图像 \(\bf x\)，Encoder 的前向调用返回均值和协方差，它们共同参数化了潜在空间中的一个（对角）高斯分布。

有了编码器和解码器网络，我们现在可以写下代表我们的模型和引导函数的随机函数。首先是模型

[ ]:

# define the model p(x|z)p(z)
def model(self, x):
    # register PyTorch module `decoder` with Pyro
    pyro.module("decoder", self.decoder)
    with pyro.plate("data", x.shape[0]):
        # setup hyperparameters for prior p(z)
        z_loc = x.new_zeros(torch.Size((x.shape[0], self.z_dim)))
        z_scale = x.new_ones(torch.Size((x.shape[0], self.z_dim)))
        # sample from prior (value will be sampled by guide when computing the ELBO)
        z = pyro.sample("latent", dist.Normal(z_loc, z_scale).to_event(1))
        # decode the latent code z
        loc_img = self.decoder(z)
        # score against actual images
        pyro.sample("obs", dist.Bernoulli(loc_img).to_event(1), obs=x.reshape(-1, 784))

注意，model() 是一个可调用对象，它将一小批图像 x 作为输入。这是一个大小为 batch_size x 784 的 torch.Tensor。

我们在 model() 内部做的第一件事是向 Pyro 注册（之前已实例化的）解码器模块。注意，我们给它一个合适（且唯一）的名称。这个对 pyro.module 的调用让 Pyro 了解解码器网络内部的所有参数。

接下来我们设置先验分布的超参数，它是一个标准正态高斯分布。请注意：- 我们通过 pyro.plate 特别指定了小批量数据（即最左维）之间的独立性。另外，请注意从潜变量 z 采样时使用 .to_event(1) - 这确保了我们的样本不是被视为从一个 batch_size = z_dim 的单变量正态分布生成，而是被视为从一个对角协方差的多变量正态分布生成。因此，当评估“潜变量”样本的 .log_prob 时，沿每个维度的对数概率会被求和。有关更多详细信息，请参阅张量形状教程。- 由于我们处理的是一整个小批量的图像，我们需要 z_loc 和 z_scale 的最左维等于小批量大小 - 如果我们在 GPU 上运行，我们使用 new_zeros 和 new_ones 来确保新创建的张量位于同一个 GPU 设备上。

接下来我们从先验分布中采样潜变量 z，确保给该随机变量一个唯一的 Pyro 名称 'latent'。然后我们将 z 通过解码器网络，它返回 loc_img。然后，我们根据由 loc_img 参数化的伯努利似然函数对小批量观测图像 x 进行评分。注意，我们展平了 x，使得所有像素都在最右维。

就是这样！注意 model 中 Pyro 原语的流程与我们模型的生成故事（例如，图 1 所概括的）是多么紧密地一致。现在我们转向引导函数

[ ]:

# define the guide (i.e. variational distribution) q(z|x)
def guide(self, x):
    # register PyTorch module `encoder` with Pyro
    pyro.module("encoder", self.encoder)
    with pyro.plate("data", x.shape[0]):
        # use the encoder to get the parameters used to define q(z|x)
        z_loc, z_scale = self.encoder(x)
        # sample the latent code z
        pyro.sample("latent", dist.Normal(z_loc, z_scale).to_event(1))

就像在模型中一样，我们首先将正在使用的 PyTorch 模块（即 encoder）注册到 Pyro。我们获取小批量的图像 x 并将其通过编码器。然后使用编码器网络输出的参数，我们使用正态分布对小批量中每张图像的潜变量进行采样。关键的是，我们对潜随机变量使用了与模型中相同的名称：'latent'。此外，请注意使用 pyro.plate 指定小批量维度的独立性，以及使用 .to_event(1) 强制依赖于 z_dims，这与我们在模型中的做法完全一致。

现在我们已经定义了完整的模型和引导函数，可以继续进行推断了。但在这样做之前，让我们看看如何在 PyTorch 模块中打包模型和引导函数

[ ]:

class VAE(nn.Module):
    # by default our latent space is 50-dimensional
    # and we use 400 hidden units
    def __init__(self, z_dim=50, hidden_dim=400, use_cuda=False):
        super().__init__()
        # create the encoder and decoder networks
        self.encoder = Encoder(z_dim, hidden_dim)
        self.decoder = Decoder(z_dim, hidden_dim)

        if use_cuda:
            # calling cuda() here will put all the parameters of
            # the encoder and decoder networks into gpu memory
            self.cuda()
        self.use_cuda = use_cuda
        self.z_dim = z_dim

    # define the model p(x|z)p(z)
    def model(self, x):
        # register PyTorch module `decoder` with Pyro
        pyro.module("decoder", self.decoder)
        with pyro.plate("data", x.shape[0]):
            # setup hyperparameters for prior p(z)
            z_loc = x.new_zeros(torch.Size((x.shape[0], self.z_dim)))
            z_scale = x.new_ones(torch.Size((x.shape[0], self.z_dim)))
            # sample from prior (value will be sampled by guide when computing the ELBO)
            z = pyro.sample("latent", dist.Normal(z_loc, z_scale).to_event(1))
            # decode the latent code z
            loc_img = self.decoder(z)
            # score against actual images
            pyro.sample("obs", dist.Bernoulli(loc_img).to_event(1), obs=x.reshape(-1, 784))

    # define the guide (i.e. variational distribution) q(z|x)
    def guide(self, x):
        # register PyTorch module `encoder` with Pyro
        pyro.module("encoder", self.encoder)
        with pyro.plate("data", x.shape[0]):
            # use the encoder to get the parameters used to define q(z|x)
            z_loc, z_scale = self.encoder(x)
            # sample the latent code z
            pyro.sample("latent", dist.Normal(z_loc, z_scale).to_event(1))

    # define a helper function for reconstructing images
    def reconstruct_img(self, x):
        # encode image x
        z_loc, z_scale = self.encoder(x)
        # sample in latent space
        z = dist.Normal(z_loc, z_scale).sample()
        # decode the image (note we don't sample in image space)
        loc_img = self.decoder(z)
        return loc_img

我们在此要说明的是，两个 Modules encoder 和 decoder 是 VAE（它本身继承自 nn.Module）的属性。这意味着它们都会自动注册为属于 VAE 模块。因此，例如，当我们在 VAE 的一个实例上调用 parameters() 时，PyTorch 会知道返回所有相关的参数。这也意味着，如果我们正在 GPU 上运行，调用 cuda() 会将所有（子）模块的所有参数移到 GPU 内存中。

推断¶

现在我们准备好进行推断了。请参阅下一节中的完整代码。

首先我们实例化 VAE 模块的一个实例。

[ ]:

vae = VAE()

然后我们设置 Adam 优化器的一个实例。

[ ]:

optimizer = Adam({"lr": 1.0e-3})

然后我们设置我们的推断算法，它将通过最大化 ELBO 来学习模型和引导函数的良好参数

[ ]:

svi = SVI(vae.model, vae.guide, optimizer, loss=Trace_ELBO())

就是这样。现在我们只需定义训练循环

[ ]:

def train(svi, train_loader, use_cuda=False):
    # initialize loss accumulator
    epoch_loss = 0.
    # do a training epoch over each mini-batch x returned
    # by the data loader
    for x, _ in train_loader:
        # if on GPU put mini-batch into CUDA memory
        if use_cuda:
            x = x.cuda()
        # do ELBO gradient and accumulate loss
        epoch_loss += svi.step(x)

    # return epoch loss
    normalizer_train = len(train_loader.dataset)
    total_epoch_loss_train = epoch_loss / normalizer_train
    return total_epoch_loss_train

请注意，所有小批量逻辑都由数据加载器处理。训练循环的核心是 svi.step(x)。这里有两点需要注意

传递给 step 的任何参数都会传递给模型和引导函数。因此，model 和 guide 需要具有相同的调用签名
step 返回损失（即 ELBO 的负数）的一个带噪声的估计。这个估计没有经过任何归一化，所以例如它会随小批量的大小而变化

添加评估逻辑的方法类似

[ ]:

def evaluate(svi, test_loader, use_cuda=False):
    # initialize loss accumulator
    test_loss = 0.
    # compute the loss over the entire test set
    for x, _ in test_loader:
        # if on GPU put mini-batch into CUDA memory
        if use_cuda:
            x = x.cuda()
        # compute ELBO estimate and accumulate loss
        test_loss += svi.evaluate_loss(x)
    normalizer_test = len(test_loader.dataset)
    total_epoch_loss_test = test_loss / normalizer_test
    return total_epoch_loss_test

基本上我们唯一需要做的改变是调用 evaluate_loss 而不是 step。这个函数将计算 ELBO 的一个估计值，但不会执行任何梯度步长。

我们想强调的最后一段代码是 VAE 类中的 helper 方法 reconstruct_img：这只是我们将引言中描述的图像重建实验翻译成了代码。我们取一张图像，将其通过编码器。然后，使用编码器提供的高斯分布在潜在空间进行采样。最后，我们将潜在代码解码成一张图像：我们返回均值向量 loc_img，而不是用它进行采样。请注意，由于 sample() 语句是随机的，每次运行 reconstruct_img 函数时，我们都会得到不同的 z 样本。如果我们学到了一个好的模型和引导函数——特别是如果我们学到了一个好的潜在表示——这些 z 样本的多样性将对应于不同风格的数字书写，重建的图像应该会展现出有趣的各种不同风格。

代码和样本结果¶

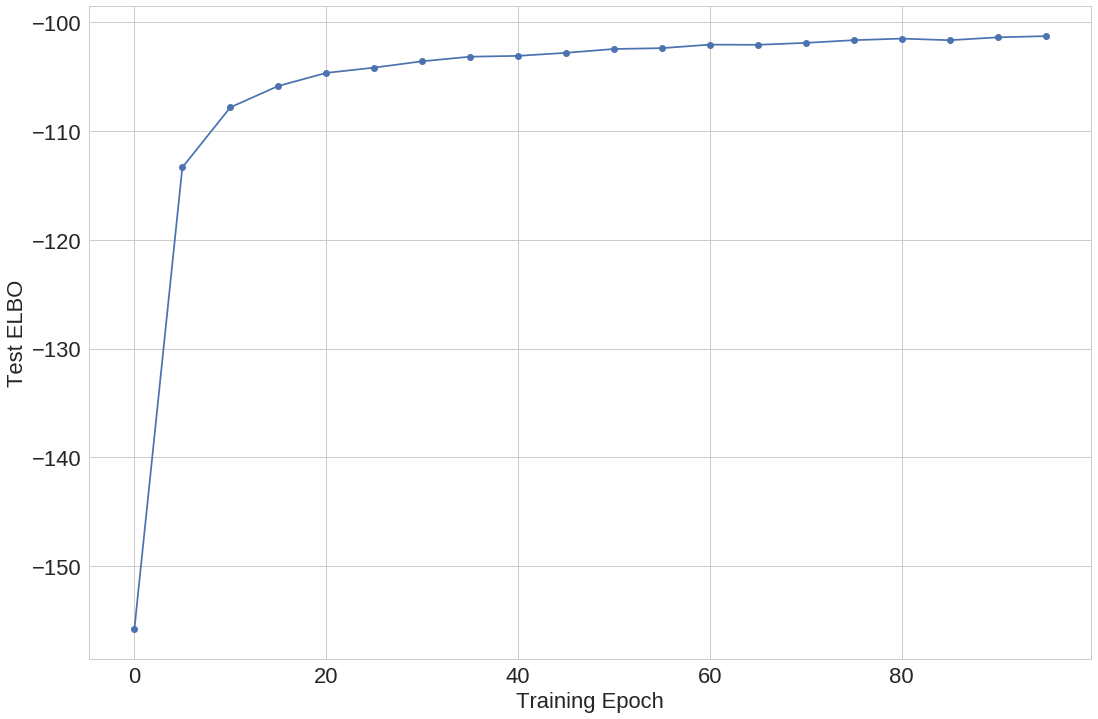
训练对应于最大化训练数据集上的证据下界 (ELBO)。我们训练 100 次迭代，并评估测试数据集的 ELBO，见图 3。

[ ]:

# Run options
LEARNING_RATE = 1.0e-3
USE_CUDA = False

# Run only for a single iteration for testing
NUM_EPOCHS = 1 if smoke_test else 100
TEST_FREQUENCY = 5

[ ]:

train_loader, test_loader = setup_data_loaders(batch_size=256, use_cuda=USE_CUDA)

# clear param store
pyro.clear_param_store()

# setup the VAE
vae = VAE(use_cuda=USE_CUDA)

# setup the optimizer
adam_args = {"lr": LEARNING_RATE}
optimizer = Adam(adam_args)

# setup the inference algorithm
svi = SVI(vae.model, vae.guide, optimizer, loss=Trace_ELBO())

train_elbo = []
test_elbo = []
# training loop
for epoch in range(NUM_EPOCHS):
    total_epoch_loss_train = train(svi, train_loader, use_cuda=USE_CUDA)
    train_elbo.append(-total_epoch_loss_train)
    print("[epoch %03d]  average training loss: %.4f" % (epoch, total_epoch_loss_train))

    if epoch % TEST_FREQUENCY == 0:
        # report test diagnostics
        total_epoch_loss_test = evaluate(svi, test_loader, use_cuda=USE_CUDA)
        test_elbo.append(-total_epoch_loss_test)
        print("[epoch %03d] average test loss: %.4f" % (epoch, total_epoch_loss_test))

接下来我们展示了一组从模型中随机采样的图像。这些图像是通过随机抽取 z 的样本并为每个样本生成一张图像来生成的，见图 4。

我们还通过编码所有 MNIST 图像并将其均值嵌入到 2 维 T-SNE 空间中，研究了整个测试数据集的 50 维潜在空间。然后我们根据图像的类别对每个嵌入图像进行着色。结果如图 5 所示，按类别进行了分离，每个类别簇内存在方差。

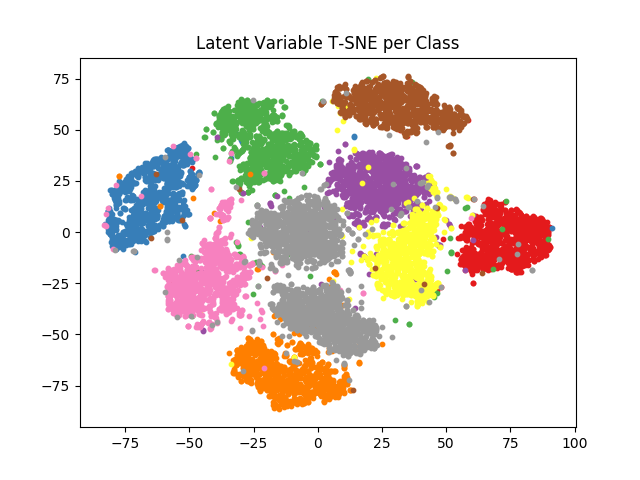
完整代码请参见 Github。

参考文献¶

[1] Auto-Encoding Variational Bayes, Diederik P Kingma, Max Welling

[2] Stochastic Backpropagation and Approximate Inference in Deep Generative Models, Danilo Jimenez Rezende, Shakir Mohamed, Daan Wierstra