Pyro 中的 Dirichlet 过程混合模型

什么是贝叶斯非参数模型？

贝叶斯非参数模型是参数数量随着提供的数据量自由增长的模型；因此，无需训练多个复杂度不同的模型并进行比较，而是可以设计一个模型，其复杂度随着观察到的数据增多而增长。贝叶斯非参数学在实践中的典型例子是 Dirichlet 过程混合模型 (DPMM)。当数据几何结构中的不同聚类数量未知时，DPMM 允许实践者构建混合模型——换句话说，聚类数量可以随着观察到的数据增多而增长。这一特性使得 DPMM 在探索性数据分析中非常有用，因为在探索性数据分析中，数据本身的已知方面很少；本文旨在证明这一事实。

Dirichlet 过程（Ferguson，1973）

Dirichlet 过程是一族定义在离散概率分布上的概率分布。形式上，Dirichlet 过程 (DP) 由某个基础概率分布 \(G_0: \Omega \to \mathbb{R}\) 和一个正实数缩放参数（通常记为 \(\alpha\)）指定。从参数为 \(G_0: \Omega \to \mathbb{R}\) 和 \(\alpha\) 的 Dirichlet 过程中抽取的样本 \(G\) 本身是定义在 \(\Omega\) 上的分布。对于 \(\Omega\) 的任意不相交划分 \(\Omega_1, ..., \Omega_k\)，以及任意样本 \(G \sim DP(G_0, \alpha)\)，我们有

\[(G(\Omega_1), ..., G(\Omega_k)) \sim \text{Dir}(\alpha G_0(\Omega_1), ..., \alpha G_0(\Omega_k))\]

本质上，这是对样本空间 \(\Omega\) 进行离散划分，然后使用基础分布 \(G_0\) 在其上构建离散分布。尽管形式上相当抽象，Dirichlet 过程作为各种图模型中的先验非常有用。在以下方案中，这一点更容易理解。

中餐馆过程（Aldous，1985）

想象一家拥有无限张桌子（用正整数索引）的餐厅，它一次只接待一位顾客。第 \(n\) 位顾客根据以下概率选择座位

• 以概率 \(\frac{n_t}{\alpha + n - 1}\) 坐在桌子 \(t\)，其中 \(n_t\) 是桌子 \(t\) 的人数

• 以概率 \(\frac{\alpha}{\alpha + n - 1}\) 坐在一张空桌子

如果我们将每个桌子 \(t\) 与从 \(\Omega\) 上的基础分布 \(G_0\) 中抽取的一个样本关联起来，然后将非归一化概率质量 \(n_t\) 关联到该样本，那么由此产生的在 \(\Omega\) 上的分布等价于从 Dirichlet 过程 \(DP(G_0, \alpha)\) 中抽取的一个样本。

此外，我们可以很容易地将其扩展来定义非参数混合模型的生成过程：每个至少有一位顾客就座的桌子 \(t\) 都关联着一组聚类参数 \(\theta_t\)，这些参数本身是从某个基础分布 \(G_0\) 中抽取的。对于每个新的观测值，首先根据上述概率将其分配到一张桌子；然后，该观测值从由该桌子聚类参数化的分布中抽取。如果观测值被分配到一张新桌子，则从 \(G_0\) 中抽取一组新的聚类参数，然后从由这些聚类参数化的分布中抽取观测值。

虽然这种 Dirichlet 过程混合模型的公式很直观，但在概率编程框架中进行推断却非常困难。这促使人们提出了 DPMM 的另一种公式，经验表明这种公式更有利于推断（例如 Blei 和 Jordan，2004）。

拆棍法（Sethuraman，1994）

DPMM 拆棍法的生成过程如下

• 对于 \(i \in \mathbb{N}\)，抽取 \(\beta_i \sim \text{Beta}(1, \alpha)\)

• 对于 \(i \in \mathbb{N}\)，抽取 \(\theta_i \sim G_0\)

• 通过 \(\pi_i(\beta_{1:\infty}) = \beta_i \prod_{j<i} (1-\beta_j)\) 构建混合权重 \(\pi\)

• 对于每个观测值 \(n \in \{1, ..., N\}\)，抽取 \(z_n \sim \pi(\beta_{1:\infty})\)，然后抽取 \(x_n \sim f(\theta_{z_n})\)

在这里，Dirichlet 过程混合模型的无限性更容易看到。此外，所有的 \(\beta_i\) 都是独立的，因此在概率编程框架中进行推断要容易得多。

首先，我们导入所有需要的模块

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from tqdm import tqdm

import torch
import torch.nn.functional as F
from torch.distributions import constraints

import pyro
from pyro.distributions import *
from pyro.infer import Predictive, SVI, Trace_ELBO
from pyro.optim import Adam

assert pyro.__version__.startswith('1.9.1')
pyro.set_rng_seed(0)

推断

合成高斯混合模型

我们首先在一个由四个二维高斯混合生成的合成数据集上演示 Dirichlet 过程混合模型的能力

data = torch.cat((MultivariateNormal(-8 * torch.ones(2), torch.eye(2)).sample([50]),
                  MultivariateNormal(8 * torch.ones(2), torch.eye(2)).sample([50]),
                  MultivariateNormal(torch.tensor([1.5, 2]), torch.eye(2)).sample([50]),
                  MultivariateNormal(torch.tensor([-0.5, 1]), torch.eye(2)).sample([50])))

plt.scatter(data[:, 0], data[:, 1])
plt.title("Data Samples from Mixture of 4 Gaussians")
plt.show()
N = data.shape[0]

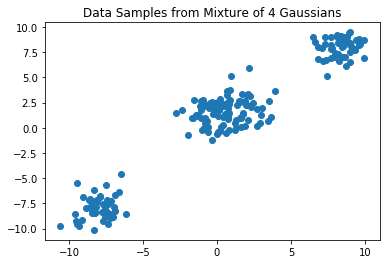
在此示例中，聚类参数 \(\theta_i\) 是描述具有单位协方差的多变量高斯均值的二维向量。因此，Dirichlet 过程基础分布 \(G_0\) 也是一个多变量高斯（即共轭先验），尽管此选择在计算上并不那么有用，因为我们并非执行坐标上升变分推断，而是使用 Pyro 执行黑盒变分推断。

首先，我们定义根据抽取的 \(\beta\) 生成权重的“拆棍”函数

def mix_weights(beta):
    beta1m_cumprod = (1 - beta).cumprod(-1)
    return F.pad(beta, (0, 1), value=1) * F.pad(beta1m_cumprod, (1, 0), value=1)

接下来，我们定义我们的模型。参考本教程第一部分中介绍的拆棍法模型定义可能会有所帮助。

注意，所有的 \(\beta_i\) 样本是条件独立的，因此我们使用大小为 T-1 的 pyro.plate 对它们进行建模；对于所有聚类参数 \(\mu_i\) 的样本，我们也这样做。然后，我们使用下方（第 9 行）抽取的 \(\beta\) 值构建一个参数为混合权重的 Categorical 分布，并从该 Categorical 分布中为每个数据点抽取聚类分配 \(z_n\)。最后，我们从一个多变量高斯分布中抽取观测值，其均值正是与我们为点 \(x_n\) 抽取的分配 \(z_n\) 相对应的聚类参数。这可以在下面的 Pyro 代码中看到

def model(data):
    with pyro.plate("beta_plate", T-1):
        beta = pyro.sample("beta", Beta(1, alpha))

    with pyro.plate("mu_plate", T):
        mu = pyro.sample("mu", MultivariateNormal(torch.zeros(2), 5 * torch.eye(2)))

    with pyro.plate("data", N):
        z = pyro.sample("z", Categorical(mix_weights(beta)))
        pyro.sample("obs", MultivariateNormal(mu[z], torch.eye(2)), obs=data)

现在，是时候定义我们的引导并执行推断了。

我们在变分推断中优化的变分族 \(q(\beta, \theta, z)\) 由下式给出

\[q(\beta, \theta, z) = \prod_{t=1}^{T-1} q_t(\beta_t) \prod_{t=1}^T q_t(\theta_t) \prod_{n=1}^N q_n(z_n)\]

注意，由于我们无法在计算上对模型假设的无限聚类进行建模，我们将变分族截断到 \(T\) 个聚类。这不影响我们的模型；相反，这是在推断阶段为了实现可处理性而进行的简化。

引导完全根据上面定义的变分族 \(q(\beta, \theta, z)\) 构建。对于模型中抽取的每个 \(\beta\)，我们有 \(T-1\) 个条件独立的 Beta 分布；对于每个聚类参数 \(\mu_i\)，我们有 \(T\) 个条件独立的多变量高斯分布；对于每个聚类分配 \(z_n\)，我们有 \(N\) 个条件独立的 Categorical 分布。

因此，我们的变分参数 (pyro.param) 包括参数化变分 Beta 分布第二个参数的 \(T-1\) 个正标量（第一个形状参数固定为 \(1\)，如模型定义所示），参数化变分多变量高斯分布的 \(T\) 个二维向量（我们不对高斯分布的协方差矩阵进行参数化，尽管在分析真实数据集时为了更大的灵活性应该这样做），以及参数化变分 Categorical 分布的 \(N\) 个 \(T\) 维向量。

def guide(data):
    kappa = pyro.param('kappa', lambda: Uniform(0, 2).sample([T-1]), constraint=constraints.positive)
    tau = pyro.param('tau', lambda: MultivariateNormal(torch.zeros(2), 3 * torch.eye(2)).sample([T]))
    phi = pyro.param('phi', lambda: Dirichlet(1/T * torch.ones(T)).sample([N]), constraint=constraints.simplex)

    with pyro.plate("beta_plate", T-1):
        q_beta = pyro.sample("beta", Beta(torch.ones(T-1), kappa))

    with pyro.plate("mu_plate", T):
        q_mu = pyro.sample("mu", MultivariateNormal(tau, torch.eye(2)))

    with pyro.plate("data", N):
        z = pyro.sample("z", Categorical(phi))

进行推断时，我们将数据集中的最大聚类数‘猜测’设置为 \(T = 6\)。我们定义了优化算法 (pyro.optim.Adam) 以及 Pyro SVI 对象，并训练模型 1000 次迭代。

执行推断后，我们构建均值的贝叶斯估计（变分近似中每个因子的期望值），并将其红色绘制在原始数据集之上。注意，我们还根据学习到的变分分布移除了分配权重小于某个阈值的聚类，然后重新归一化权重使其总和为一。

T = 6
optim = Adam({"lr": 0.05})
svi = SVI(model, guide, optim, loss=Trace_ELBO())
losses = []

def train(num_iterations):
    pyro.clear_param_store()
    for j in tqdm(range(num_iterations)):
        loss = svi.step(data)
        losses.append(loss)

def truncate(alpha, centers, weights):
    threshold = alpha**-1 / 100.
    true_centers = centers[weights > threshold]
    true_weights = weights[weights > threshold] / torch.sum(weights[weights > threshold])
    return true_centers, true_weights

alpha = 0.1
train(1000)

# We make a point-estimate of our model parameters using the posterior means of tau and phi for the centers and weights
Bayes_Centers_01, Bayes_Weights_01 = truncate(alpha, pyro.param("tau").detach(), torch.mean(pyro.param("phi").detach(), dim=0))

alpha = 1.5
train(1000)

# We make a point-estimate of our model parameters using the posterior means of tau and phi for the centers and weights
Bayes_Centers_15, Bayes_Weights_15 = truncate(alpha, pyro.param("tau").detach(), torch.mean(pyro.param("phi").detach(), dim=0))

plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
plt.scatter(data[:, 0], data[:, 1], color="blue")
plt.scatter(Bayes_Centers_01[:, 0], Bayes_Centers_01[:, 1], color="red")

plt.subplot(1, 2, 2)
plt.scatter(data[:, 0], data[:, 1], color="blue")
plt.scatter(Bayes_Centers_15[:, 0], Bayes_Centers_15[:, 1], color="red")
plt.tight_layout()
plt.show()

100%|██████████| 1000/1000 [00:15<00:00, 64.86it/s]
100%|██████████| 1000/1000 [00:15<00:00, 65.47it/s]

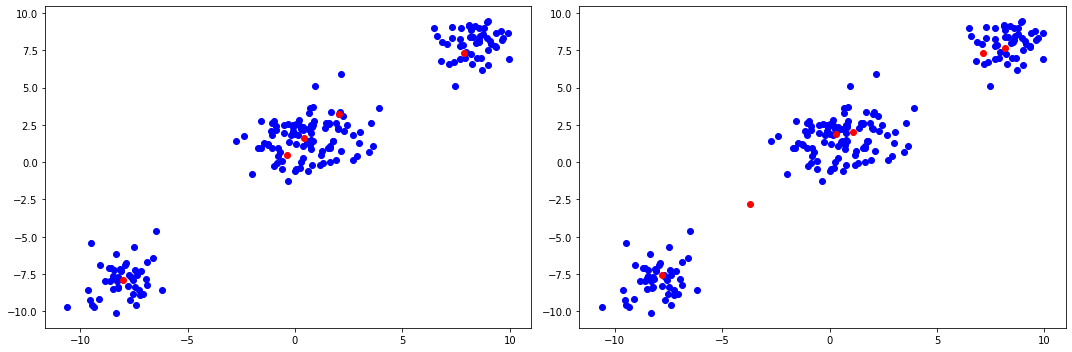
上面的图展示了缩放超参数 \(\alpha\) 的影响。较大的 \(\alpha\) 会产生权重更重尾的分布，而较小的 \(\alpha\) 会将更多质量集中在更少的聚类上。特别是，中间的聚类看起来可能由一个高斯生成（尽管实际上是由两个不同的高斯生成），因此 \(\alpha\) 的设置允许实践者进一步编码他们关于数据包含多少聚类的先验信念。

用于长期太阳观测的 Dirichlet 混合模型

如前所述，当探索一个潜在几何结构完全未知的数据集时，Dirichlet 过程混合模型真正大放异彩。为了证明这一点，我们在过去 300 年的太阳黑子计数数据（由比利时皇家天文台提供）上拟合了一个 DPMM。

df = pd.read_csv('http://www.sidc.be/silso/DATA/SN_y_tot_V2.0.csv', sep=';', names=['time', 'sunspot.year'], usecols=[0, 1])
data = torch.tensor(df['sunspot.year'].values, dtype=torch.float32).round()
N = data.shape[0]

plt.hist(df['sunspot.year'].values, bins=40)
plt.title("Number of Years vs. Sunspot Counts")
plt.xlabel("Sunspot Count")
plt.ylabel("Number of Years")
plt.show()

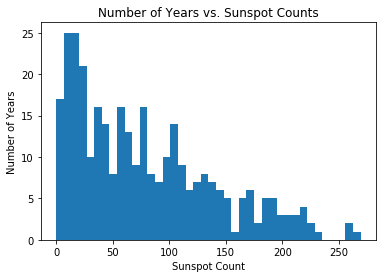
对于这个例子，聚类参数 \(\theta_i\) 是速率参数，因为我们正在构建 Poisson 分布的尺度混合。同样，\(G_0\) 选择为共轭先验，在本例中是 Gamma 分布，尽管通过 Pyro 进行推断时这并不严格重要。下面是模型的实现

def model(data):
    with pyro.plate("beta_plate", T-1):
        beta = pyro.sample("beta", Beta(1, alpha))

    with pyro.plate("lambda_plate", T):
        lmbda = pyro.sample("lambda", Gamma(3, 0.05))

    with pyro.plate("data", N):
        z = pyro.sample("z", Categorical(mix_weights(beta)))
        pyro.sample("obs", Poisson(lmbda[z]), obs=data)

def guide(data):
    kappa = pyro.param('kappa', lambda: Uniform(0, 2).sample([T-1]), constraint=constraints.positive)
    tau_0 = pyro.param('tau_0', lambda: Uniform(0, 5).sample([T]), constraint=constraints.positive)
    tau_1 = pyro.param('tau_1', lambda: LogNormal(-1, 1).sample([T]), constraint=constraints.positive)
    phi = pyro.param('phi', lambda: Dirichlet(1/T * torch.ones(T)).sample([N]), constraint=constraints.simplex)

    with pyro.plate("beta_plate", T-1):
        q_beta = pyro.sample("beta", Beta(torch.ones(T-1), kappa))

    with pyro.plate("lambda_plate", T):
        q_lambda = pyro.sample("lambda", Gamma(tau_0, tau_1))

    with pyro.plate("data", N):
        z = pyro.sample("z", Categorical(phi))

T = 20
alpha = 1.1
n_iter = 1500
optim = Adam({"lr": 0.05})
svi = SVI(model, guide, optim, loss=Trace_ELBO())
losses = []

train(n_iter)

samples = torch.arange(0, 300).type(torch.float)

tau0_optimal = pyro.param("tau_0").detach()
tau1_optimal = pyro.param("tau_1").detach()
kappa_optimal = pyro.param("kappa").detach()

# We make a point-estimate of our latent variables using the posterior means of tau and kappa for the cluster params and weights
Bayes_Rates = (tau0_optimal / tau1_optimal)
Bayes_Weights = mix_weights(1. / (1. + kappa_optimal))

def mixture_of_poisson(weights, rates, samples):
    return (weights * Poisson(rates).log_prob(samples.unsqueeze(-1)).exp()).sum(-1)

likelihood = mixture_of_poisson(Bayes_Weights, Bayes_Rates, samples)

plt.title("Number of Years vs. Sunspot Counts")
plt.hist(data.numpy(), bins=60, density=True, lw=0, alpha=0.75);
plt.plot(samples, likelihood, label="Estimated Mixture Density")
plt.legend()
plt.show()

100%|██████████| 1500/1500 [00:09<00:00, 156.27it/s]

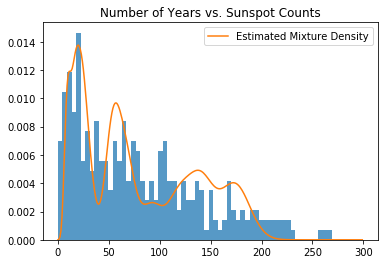
上图是聚类参数贝叶斯估计的混合密度，按其对应权重加权。与高斯示例一样，我们通过计算 lambda 和 beta 的后验均值来获得每个聚类参数及其对应权重的贝叶斯估计。

ELBO 行为

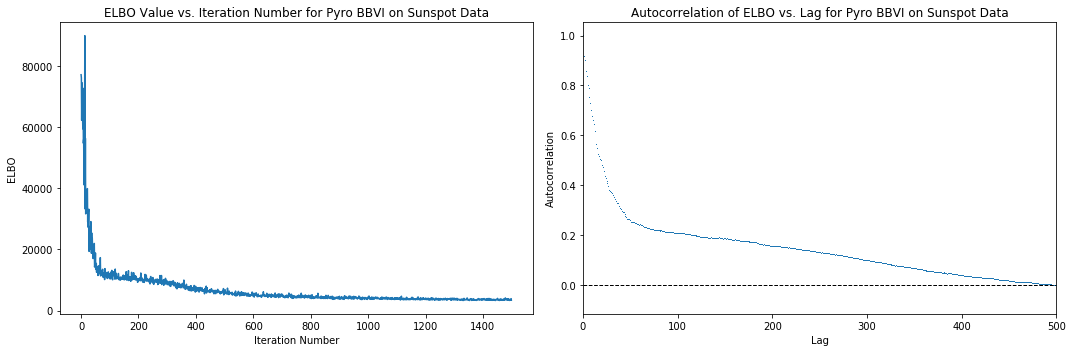
下面是在使用 Pyro 进行推断期间，SVI 迭代过程中损失函数（负 Trace_ELBO）行为的图，以及 ELBO“时间序列”自相关性与迭代次数的关系图。我们可以看到，在大约 500 次迭代后，损失停止显著下降，因此我们可以假设需要大约 500 次迭代才能达到收敛。自相关图在滞后 500 左右时，自相关性接近于 0，进一步证实了这一假设。请注意，这些都是启发式方法，不一定意味着收敛。

elbo_plot = plt.figure(figsize=(15, 5))

elbo_ax = elbo_plot.add_subplot(1, 2, 1)
elbo_ax.set_title("ELBO Value vs. Iteration Number for Pyro BBVI on Sunspot Data")
elbo_ax.set_ylabel("ELBO")
elbo_ax.set_xlabel("Iteration Number")
elbo_ax.plot(np.arange(n_iter), losses)

autocorr_ax = elbo_plot.add_subplot(1, 2, 2)
autocorr_ax.acorr(np.asarray(losses), detrend=lambda x: x - x.mean(), maxlags=750, usevlines=False, marker=',')
autocorr_ax.set_xlim(0, 500)
autocorr_ax.axhline(0, ls="--", c="k", lw=1)
autocorr_ax.set_title("Autocorrelation of ELBO vs. Lag for Pyro BBVI on Sunspot Data")
autocorr_ax.set_xlabel("Lag")
autocorr_ax.set_ylabel("Autocorrelation")
elbo_plot.tight_layout()
plt.show()

模型评估

长期太阳黑子模型

由于我们计算了拟合长期太阳黑子数据的 DPMM 的近似后验，我们可以利用一些内在指标，例如对数预测、后验离散度指数和后验预测检查。

由于 Dirichlet 过程混合模型的后验预测分布本身是具有解析近似的尺度混合分布 （Blei 和 Jordan，2004），这使得它特别适合上述指标

\[p(x_{new} | X_{1:N}, \alpha, G_0) \approx \sum_{t=1}^T \mathbb{E}_q [\pi_t(\beta)] \ \mathbb{E}_q \left[p(x_{new} | \theta_t)\right].\]

特别地，要计算对数预测，我们首先在使用数据的训练子样本对模型进行变分推断后，计算后验预测分布（如上定义）。然后，对数预测就是在测试子样本中每个点处评估的预测密度的对数值

\[\log p(x_{new} | X) = \log \mathbb{E}_{\beta, \theta | X} \left[ p(x_{new} | \beta, \theta) \right]\]

由于训练样本和测试样本都来自同一个数据集，我们期望模型能够对测试样本赋予高概率，即使在推断过程中从未见过它们。这提供了一个选择超参数 \(T\)、\(\alpha\) 和 \(G_0\) 值的方法：我们应该选择使该值最大化的值。

我们在这里使用不同的 \(\alpha\) 值执行此过程，以查看最佳设置。

# Hold out 10% of our original data to test upon
df_test = df.sample(frac=0.1)
data = torch.tensor(df.drop(df_test.index)['sunspot.year'].values, dtype=torch.float).round()
data_test = torch.tensor(df_test['sunspot.year'].values, dtype=torch.float).round()
N = data.shape[0]
N_test = data_test.shape[0]

alphas = [0.05, 0.1, 0.5, 0.75, 0.9, 1., 1.25, 1.5, 2, 2.5, 3]
log_predictives = []

for val in alphas:
    alpha = val
    T = 20
    svi = SVI(model, guide, optim, loss=Trace_ELBO())
    train(500)

    S = 100 # number of Monte Carlo samples to use in posterior predictive computations

    # Using pyro's built in posterior predictive class:
    posterior = Predictive(guide, num_samples=S, return_sites=["beta", "lambda"])(data)
    post_pred_weights = mix_weights(posterior["beta"])
    post_pred_clusters = posterior["lambda"]

    # log_prob shape = N_test x S
    log_prob = (post_pred_weights.log() + Poisson(post_pred_clusters).log_prob(data.reshape(-1, 1, 1))).logsumexp(-1)
    mean_log_prob = log_prob.logsumexp(-1) - np.log(S)
    log_posterior_predictive = mean_log_prob.sum(-1)
    log_predictives.append(log_posterior_predictive)

plt.figure(figsize=(10, 5))
plt.plot(alphas, log_predictives)
plt.title("Value of the Log Predictive at Varying Alpha")
plt.show()

100%|██████████| 500/500 [00:03<00:00, 157.68it/s]
100%|██████████| 500/500 [00:03<00:00, 165.35it/s]
100%|██████████| 500/500 [00:03<00:00, 156.21it/s]
100%|██████████| 500/500 [00:03<00:00, 165.50it/s]
100%|██████████| 500/500 [00:02<00:00, 172.95it/s]
100%|██████████| 500/500 [00:02<00:00, 169.13it/s]
100%|██████████| 500/500 [00:02<00:00, 169.17it/s]
100%|██████████| 500/500 [00:02<00:00, 169.48it/s]
100%|██████████| 500/500 [00:02<00:00, 173.85it/s]
100%|██████████| 500/500 [00:02<00:00, 171.00it/s]
100%|██████████| 500/500 [00:03<00:00, 161.77it/s]

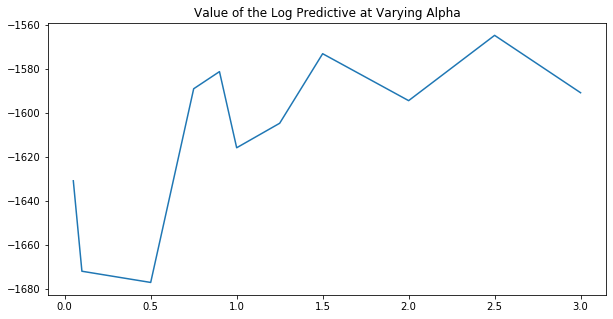
从上图中，我们可以推断出 \(\alpha > 1\) 是较好的设置，尽管信号不是很清晰。更全面的模型评估过程将涉及对所有超参数进行网格搜索，以找到使对数预测最大化的那个。

参考文献

1. Ferguson, Thomas. A Bayesian Analysis of Some Nonparametric Problems. The Annals of Statistics, Vol. 1, No. 2 (1973).

2. Aldous, D. Exchangeability and Related Topics. Ecole diete de Probabilities Saint Flour (1985).

3. Sethuraman, J. A Constructive Definition of Dirichlet Priors. Statistica, Sinica, 4:639-650 (1994).

4. Blei, David and Jordan, Michael. Variational Inference for Dirichlet Process Mixtures. Bayesian Analysis, Vol. 1, No. 1 (2004).

5. Pedregosa, et al. Scikit-Learn: Machine Learning in Python. JMLR 12, pp. 2825-2830 (2011).

6. Bishop, Christopher. Pattern Recogition and Machine Learning. Springer Ltd (2006).

7. Sunspot Index and Long-Term Solar Observations. WDC-SILSO, Royal Observatory of Belgium, Brussels (2018).

8. Gelman, Andrew. Understanding predictive information criteria for Bayesian models. Statistics and Computing, Springer Link, 2014.