编译序列重要性采样¶
编译序列重要性采样 [1],或称推断编译,是一种通过学习重要性采样的提议分布来分摊推断计算成本的技术。
提议分布被学习以最小化模型与 guide 之间的 KL 散度,\(\rm{KL}\!\left( p({\bf z} | {\bf x}) \lVert q_{\phi, x}({\bf z}) \right)\)。这与变分推断不同,变分推断会最小化 \(\rm{KL}\!\left( q_{\phi, x}({\bf z}) \lVert p({\bf z} | {\bf x}) \right)\)。使用前一种损失鼓励近似提议分布比真实的后验分布更宽(覆盖质量),而变分推断通常学习更窄的近似分布(寻找模式)。重要性采样的 guide 通常期望其尾部比模型更重(参见这个 stackexchange 问题)。因此,推断编译损失通常更适合于编译重要性采样的 guide。
CSIS 的另一个优点是,与许多类型的变分推断不同,它不要求模型是可微的。这使得它可以用于对任意复杂的程序进行推断(例如,Captcha 渲染器 [1])。
本示例展示了如何使用 CSIS 来加速对已知解析解的简单问题的推断。
[1]:
import torch
import torch.nn as nn
import torch.functional as F
import pyro
import pyro.distributions as dist
import pyro.infer
import pyro.optim
import os
smoke_test = ('CI' in os.environ)
n_steps = 2 if smoke_test else 2000
指定模型:¶
模型以与任何 Pyro 模型相同的方式指定,但必须使用关键字参数 observations 来输入一个字典,其中每个观察值作为键。由于推断编译涉及学习对任何观察值进行推断,因此字典中的值是什么并不重要。此处使用 0。
[2]:
def model(prior_mean, observations={"x1": 0, "x2": 0}):
x = pyro.sample("z", dist.Normal(prior_mean, torch.tensor(5**0.5)))
y1 = pyro.sample("x1", dist.Normal(x, torch.tensor(2**0.5)), obs=observations["x1"])
y2 = pyro.sample("x2", dist.Normal(x, torch.tensor(2**0.5)), obs=observations["x2"])
return x
指定 guide:¶
guide 将被训练(又称编译)以使用观察值来为每个未条件化的 sample 语句创建提议分布。在论文 [1] 中,神经网络结构是为任何模型自动生成的。然而,在 Pyro 的实现中,用户必须指定特定任务的 guide 程序结构。与任何 Pyro guide 函数一样,它应该具有与模型相同的调用签名。它还必须遇到与模型相同的未观测到的 sample 语句。为了使 guide 程序能够训练出好的提议分布,sample 语句处的分布应该依赖于 observations 中的值。在此示例中,使用前馈神经网络将观察值映射到隐变量的提议分布。
在运行 guide 函数时调用 pyro.module,以便优化器在训练期间可以找到 guide 参数。
[3]:
class Guide(nn.Module):
def __init__(self):
super().__init__()
self.neural_net = nn.Sequential(
nn.Linear(2, 10),
nn.ReLU(),
nn.Linear(10, 20),
nn.ReLU(),
nn.Linear(20, 10),
nn.ReLU(),
nn.Linear(10, 5),
nn.ReLU(),
nn.Linear(5, 2))
def forward(self, prior_mean, observations={"x1": 0, "x2": 0}):
pyro.module("guide", self)
x1 = observations["x1"]
x2 = observations["x2"]
v = torch.cat((x1.view(1, 1), x2.view(1, 1)), 1)
v = self.neural_net(v)
mean = v[0, 0]
std = v[0, 1].exp()
pyro.sample("z", dist.Normal(mean, std))
guide = Guide()
现在创建一个 CSIS 实例:¶
该对象使用模型、guide、用于训练 guide 的 PyTorch 优化器以及在执行推断时抽取的带权重重要性样本数量进行初始化。guide 将针对模型/guide 参数 prior_mean 的特定值进行优化,因此我们在整个训练和推断过程中都使用此处设置的值。
[4]:
optimiser = pyro.optim.Adam({'lr': 1e-3})
csis = pyro.infer.CSIS(model, guide, optimiser, num_inference_samples=50)
prior_mean = torch.tensor(1.)
现在我们“编译”该实例以对此模型执行推断:¶
传递给 csis.step 的参数在运行模型和 guide 以评估损失时传递给它们。
[5]:
for step in range(n_steps):
csis.step(prior_mean)
现在通过重要性采样执行推断:¶
编译好的 guide 程序现在应该能够为 z 提出一个近似后验分布 \(p(z | x_1, x_2)\) 的分布,适用于任何 \(x_1, x_2\)。再次输入相同的 prior_mean,以及 observations 内部的观察值。
[6]:
posterior = csis.run(prior_mean,
observations={"x1": torch.tensor(8.),
"x2": torch.tensor(9.)})
marginal = pyro.infer.EmpiricalMarginal(posterior, "z")
现在绘制结果并与重要性采样进行比较:¶
我们观察到 \(x_1 = 8\) 和 \(x_2 = 9\)。使用 CSIS 抽取 50 个样本进行推断,并使用来自先验的重要性采样抽取 50 个样本。然后绘制生成的后验分布近似图,并与解析后验进行比较。
[7]:
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt
with torch.no_grad():
# Draw samples from empirical marginal for plotting
csis_samples = torch.stack([marginal() for _ in range(1000)])
# Calculate empirical marginal with importance sampling
is_posterior = pyro.infer.Importance(model, num_samples=50).run(
prior_mean, observations={"x1": torch.tensor(8.),
"x2": torch.tensor(9.)})
is_marginal = pyro.infer.EmpiricalMarginal(is_posterior, "z")
is_samples = torch.stack([is_marginal() for _ in range(1000)])
# Calculate true prior and posterior over z
true_posterior_z = torch.arange(-10, 10, 0.05)
true_posterior_p = dist.Normal(7.25, (5/6)**0.5).log_prob(true_posterior_z).exp()
prior_z = true_posterior_z
prior_p = dist.Normal(1., 5**0.5).log_prob(true_posterior_z).exp()
plt.rcParams['figure.figsize'] = [30, 15]
plt.rcParams.update({'font.size': 30})
fig, ax = plt.subplots()
plt.plot(prior_z, prior_p, 'k--', label='Prior')
plt.plot(true_posterior_z, true_posterior_p, color='k', label='Analytic Posterior')
plt.hist(csis_samples.numpy(), range=(-10, 10), bins=100, color='r', density=1,
label="Inference Compilation")
plt.hist(is_samples.numpy(), range=(-10, 10), bins=100, color='b', density=1,
label="Importance Sampling")
plt.xlim(-8, 10)
plt.ylim(0, 5)
plt.xlabel("z")
plt.ylabel("Estimated Posterior Probability Density")
plt.legend()
plt.show()
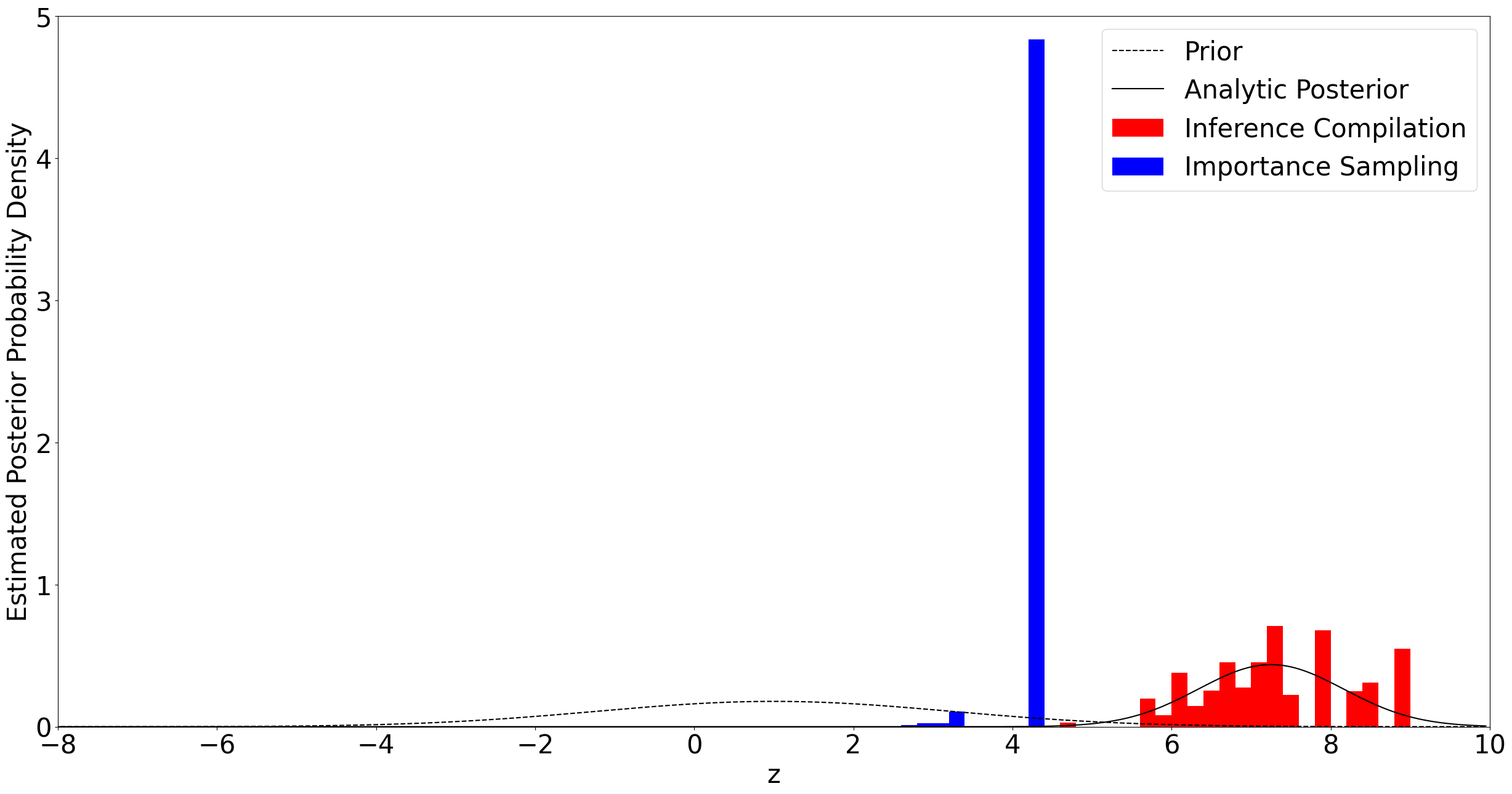
使用 \(x_1 = 8\) 和 \(x_2 = 9\) 得到的后验分布远离先验,因此使用先验作为重要性采样的 guide 是低效的,有效样本大小非常小。通过首先学习合适的 guide 函数,CSIS 具有与真实后验更匹配的提议分布。这使得抽取的样本更能覆盖真实后验,并获得更大的有效样本大小,如上图所示。
有关推断编译的其他示例,请参阅 [1] 或 https://github.com/probprog/anglican-infcomp-examples。
参考文献¶
[1] Inference compilation and universal probabilistic programming, Tuan Anh Le, Atilim Gunes Baydin, and Frank Wood