高斯过程¶
简介¶
高斯过程已应用于监督学习、无监督学习甚至强化学习问题,并由优雅的数学理论描述(有关该主题的概述,请参阅 [1, 4])。它们在概念上也极具吸引力,因为它们提供了一种直观的方式来定义函数上的先验。最后,由于高斯过程是在贝叶斯设置中表述的,它们配备了强大的不确定性概念。
令人高兴的是,Pyro 在 pyro.contrib.gp 模块中提供了一些对高斯过程的支持。本教程的目标是简要介绍该模块背景下的高斯过程 (GP)。我们将主要关注如何在 Pyro 中使用 GP 接口,有关 GP 的更多详细信息,请参阅参考文献。
我们感兴趣的模型定义为
以及
此处 \(x, x' \in\mathbf{X}\) 是输入空间中的点,\(y\in\mathbf{Y}\) 是输出空间中的点。\(f\) 是由核 \(\mathbf{K}_f\) 指定的 GP 先验的样本,表示从 \(\mathbf{X}\) 到 \(\mathbf{Y}\) 的函数。最后,\(\epsilon\) 表示高斯观测噪声。
我们将使用径向基函数核 (RBF 核) 作为我们的 GP 的核
此处 \(\sigma^2\) 和 \(l\) 是指定核的参数;具体来说,\(\sigma^2\) 是方差或幅度平方,\(l\) 是长度尺度。我们将在下方对这些参数获得一些直观理解。
导入¶
首先,我们导入必要的模块。
[1]:
import os
import matplotlib.pyplot as plt
import torch
import numpy as np
import pyro
import pyro.contrib.gp as gp
import pyro.distributions as dist
from matplotlib.animation import FuncAnimation
from mpl_toolkits.axes_grid1 import make_axes_locatable
import seaborn as sns
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
smoke_test = "CI" in os.environ # ignore; used to check code integrity in the Pyro repo
assert pyro.__version__.startswith('1.9.1')
pyro.set_rng_seed(0)
torch.set_default_tensor_type(torch.DoubleTensor)
在本教程中,我们将需要可视化 GP。因此我们定义一个辅助函数进行绘图
[2]:
# note that this helper function does three different things:
# (i) plots the observed data;
# (ii) plots the predictions from the learned GP after conditioning on data;
# (iii) plots samples from the GP prior (with no conditioning on observed data)
def plot(
plot_observed_data=False,
plot_predictions=False,
n_prior_samples=0,
model=None,
kernel=None,
n_test=500,
ax=None,
):
if ax is None:
fig, ax = plt.subplots(figsize=(12, 6))
if plot_observed_data:
ax.plot(X.numpy(), y.numpy(), "kx")
if plot_predictions:
Xtest = torch.linspace(-0.5, 5.5, n_test) # test inputs
# compute predictive mean and variance
with torch.no_grad():
if type(model) == gp.models.VariationalSparseGP:
mean, cov = model(Xtest, full_cov=True)
else:
mean, cov = model(Xtest, full_cov=True, noiseless=False)
sd = cov.diag().sqrt() # standard deviation at each input point x
ax.plot(Xtest.numpy(), mean.numpy(), "r", lw=2) # plot the mean
ax.fill_between(
Xtest.numpy(), # plot the two-sigma uncertainty about the mean
(mean - 2.0 * sd).numpy(),
(mean + 2.0 * sd).numpy(),
color="C0",
alpha=0.3,
)
if n_prior_samples > 0: # plot samples from the GP prior
Xtest = torch.linspace(-0.5, 5.5, n_test) # test inputs
noise = (
model.noise
if type(model) != gp.models.VariationalSparseGP
else model.likelihood.variance
)
cov = kernel.forward(Xtest) + noise.expand(n_test).diag()
samples = dist.MultivariateNormal(
torch.zeros(n_test), covariance_matrix=cov
).sample(sample_shape=(n_prior_samples,))
ax.plot(Xtest.numpy(), samples.numpy().T, lw=2, alpha=0.4)
ax.set_xlim(-0.5, 5.5)
数据¶
数据包含 \(20\) 个点,这些点从以下分布采样
其中 \(x\) 从区间 \([0, 5]\) 中均匀采样。
[3]:
N = 20
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(N,))
y = 0.5 * torch.sin(3 * X) + dist.Normal(0.0, 0.2).sample(sample_shape=(N,))
plot(plot_observed_data=True) # let's plot the observed data

定义模型¶
首先,我们定义一个 RBF 核,指定两个超参数 variance 和 lengthscale 的值。然后我们构建一个 GPRegression 对象。这里我们输入另一个超参数 noise,它对应于上面的 \(\epsilon\)。
[4]:
kernel = gp.kernels.RBF(
input_dim=1, variance=torch.tensor(6.0), lengthscale=torch.tensor(0.05)
)
gpr = gp.models.GPRegression(X, y, kernel, noise=torch.tensor(0.2))
让我们看看从这个 GP 函数先验中采样的样本是什么样的。请注意,这是在未根据数据进行条件化之前。这些函数采取的形状——它们的平滑度、垂直尺度等——由 GP 核控制。
[5]:
plot(model=gpr, kernel=kernel, n_prior_samples=2)
_ = plt.ylim((-8, 8))
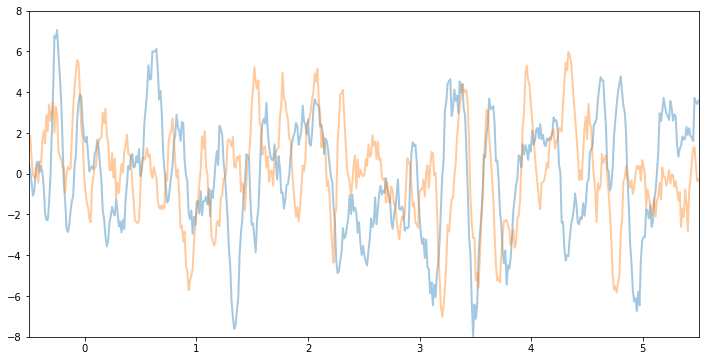
例如,如果我们保持相同的 variance 和 noise 并增加 lengthscale,我们将看到更平滑的函数样本。
[6]:
kernel2 = gp.kernels.RBF(
input_dim=1, variance=torch.tensor(6.0), lengthscale=torch.tensor(1)
)
gpr2 = gp.models.GPRegression(X, y, kernel2, noise=torch.tensor(0.2))
plot(model=gpr2, kernel=kernel2, n_prior_samples=2)
_ = plt.ylim((-8, 8))
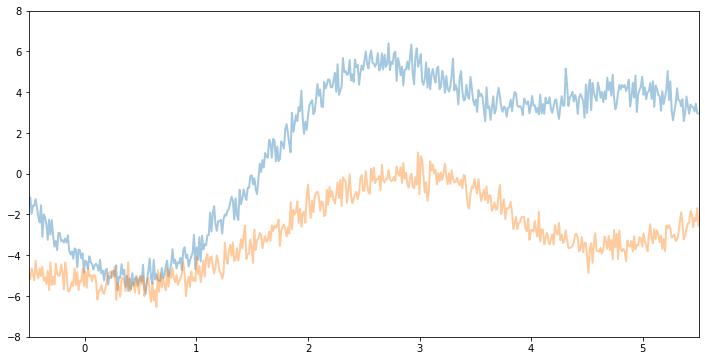
现在,如果我们减小 variance 和 noise,我们将看到垂直幅度较小的函数样本。
[7]:
kernel3 = gp.kernels.RBF(
input_dim=1, variance=torch.tensor(1.0), lengthscale=torch.tensor(1)
)
gpr3 = gp.models.GPRegression(X, y, kernel3, noise=torch.tensor(0.01))
plot(model=gpr3, kernel=kernel3, n_prior_samples=2)
_ = plt.ylim((-8, 8))
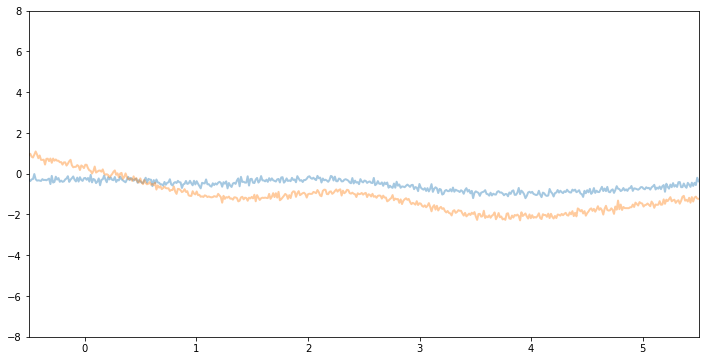
推断¶
在上面,我们手动设置了核超参数。如果我们要从数据中学习超参数,我们需要进行推断。在最简单 (共轭) 的情况下,我们对对数边缘似然进行梯度上升。在 pyro.contrib.gp 中,我们可以使用任何 PyTorch 优化器来优化模型的参数。此外,我们需要一个损失函数,它将模型和引导函数作为输入并返回 ELBO 损失(参见SVI 第一部分教程)。
[8]:
optimizer = torch.optim.Adam(gpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
variances = []
lengthscales = []
noises = []
num_steps = 2000 if not smoke_test else 2
for i in range(num_steps):
variances.append(gpr.kernel.variance.item())
noises.append(gpr.noise.item())
lengthscales.append(gpr.kernel.lengthscale.item())
optimizer.zero_grad()
loss = loss_fn(gpr.model, gpr.guide)
loss.backward()
optimizer.step()
losses.append(loss.item())
[9]:
# let's plot the loss curve after 2000 steps of training
def plot_loss(loss):
plt.plot(loss)
plt.xlabel("Iterations")
_ = plt.ylabel("Loss") # supress output text
plot_loss(losses)
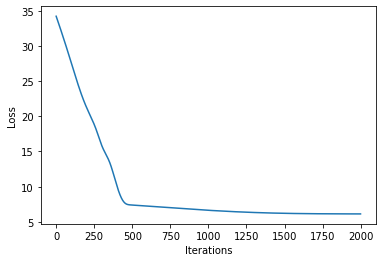
看看我们是否学到了一些合理的东西
[10]:
plot(model=gpr, plot_observed_data=True, plot_predictions=True)
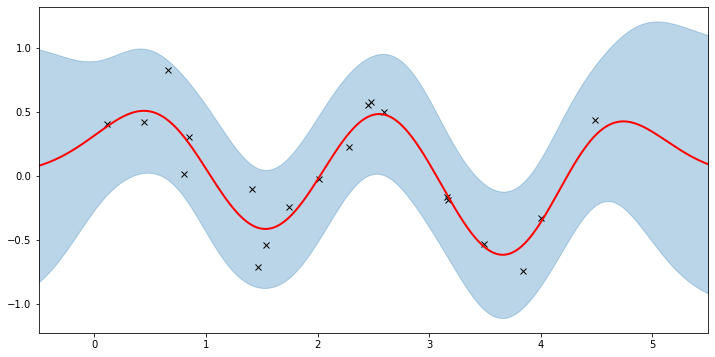
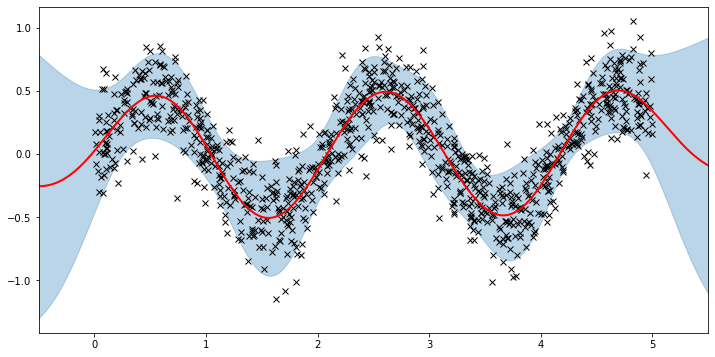
这里的粗红色曲线是平均预测值,蓝色带表示围绕平均值的 2-sigma 不确定性。看来我们学习到了合理的核超参数,因为平均值和不确定性都能很好地拟合数据。(请注意,如果我们选择了过大的学习率或选择了糟糕的初始超参数,学习过程很容易出错。)
请注意,只有当 variance 和 lengthscale 为正时,核才具有良好的定义。在底层,Pyro 使用 PyTorch 约束(参见文档)来确保超参数被约束到适当的域。让我们看看我们学到的受约束的值。
[11]:
gpr.kernel.variance.item()
[11]:
0.21701954305171967
[12]:
gpr.kernel.lengthscale.item()
[12]:
0.513454258441925
[13]:
gpr.noise.item()
[13]:
0.04248063638806343
生成数据的正弦波的周期为 \(T = 2\pi/3 \approx 2.09\),因此学习近似等于四分之一个周期的长度尺度是有意义的。现在让我们尝试通过动画来看看我们的模型在训练迭代中如何改进。
[14]:
fig, ax = plt.subplots(figsize=(12, 6))
def update(iteration):
pyro.clear_param_store()
ax.cla()
kernel_iter = gp.kernels.RBF(
input_dim=1,
variance=torch.tensor(variances[iteration]),
lengthscale=torch.tensor(lengthscales[iteration]),
)
gpr_iter = gp.models.GPRegression(
X, y, kernel_iter, noise=torch.tensor(noises[iteration])
)
plot(model=gpr_iter, plot_observed_data=True, plot_predictions=True, ax=ax)
ax.set_title(f"Iteration: {iteration}, Loss: {losses[iteration]:0.2f}")
anim = FuncAnimation(fig, update, frames=np.arange(0, num_steps, 30), interval=100)
plt.close()
anim.save("../source/_static/img/gpr-fit.gif", fps=60)

使用 MAP 拟合模型¶
我们需要为超参数定义先验。
[15]:
# Define the same model as before.
pyro.clear_param_store()
kernel = gp.kernels.RBF(
input_dim=1, variance=torch.tensor(5.0), lengthscale=torch.tensor(10.0)
)
gpr = gp.models.GPRegression(X, y, kernel, noise=torch.tensor(1.0))
# note that our priors have support on the positive reals
gpr.kernel.lengthscale = pyro.nn.PyroSample(dist.LogNormal(0.0, 1.0))
gpr.kernel.variance = pyro.nn.PyroSample(dist.LogNormal(0.0, 1.0))
optimizer = torch.optim.Adam(gpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
num_steps = 2000 if not smoke_test else 2
for i in range(num_steps):
optimizer.zero_grad()
loss = loss_fn(gpr.model, gpr.guide)
loss.backward()
optimizer.step()
losses.append(loss.item())
plot_loss(losses)
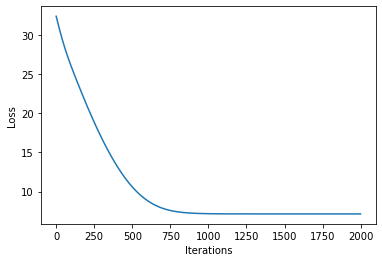
[16]:
plot(model=gpr, plot_observed_data=True, plot_predictions=True)
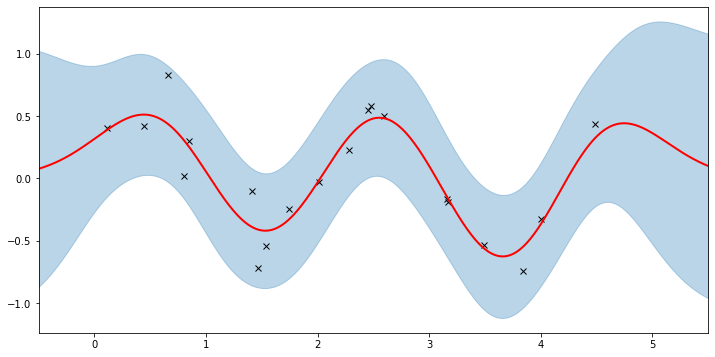
让我们检查一下我们学习到的超参数
[17]:
# tell gpr that we want to get samples from guides
gpr.set_mode("guide")
print("variance = {}".format(gpr.kernel.variance))
print("lengthscale = {}".format(gpr.kernel.lengthscale))
print("noise = {}".format(gpr.noise))
variance = 0.24472779035568237
lengthscale = 0.5217776894569397
noise = 0.042222216725349426
注意,MAP 值与 MLE 值因先验而异。
稀疏 GP¶
对于大型数据集,由于涉及昂贵的矩阵运算,计算对数边缘似然的成本很高(例如,参见 [1] 的第 2.2 节)。已经开发了各种所谓的“稀疏”变分方法,以使 GP 适用于更大的数据集。这是一个很大的研究领域,我们将不深入讨论所有细节。相反,我们将快速展示如何在 pyro.contrib.gp 中使用 SparseGPRegression 来利用这些方法。
首先,我们生成更多数据。
[18]:
N = 1000
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(N,))
y = 0.5 * torch.sin(3 * X) + dist.Normal(0.0, 0.2).sample(sample_shape=(N,))
plot(plot_observed_data=True)
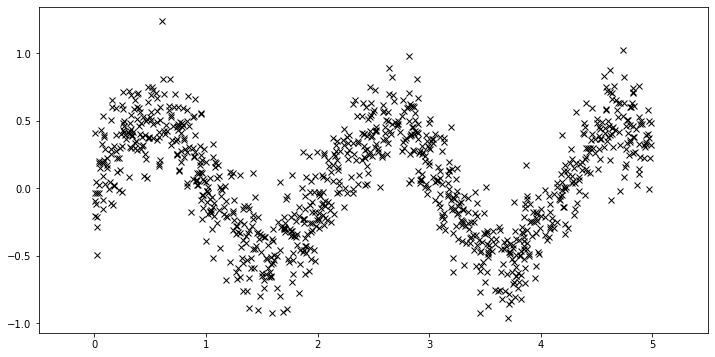
使用稀疏 GP 与使用上面基本 GP 非常相似。我们只需要添加一个额外的参数 \(X_u\)(诱导点)。让我们均匀初始化诱导点。在学习过程中,我们还将优化这些诱导点的位置。
[19]:
N = 1000
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(N,))
y = 0.5 * torch.sin(3 * X) + dist.Normal(0.0, 0.2).sample(sample_shape=(N,))
plot(plot_observed_data=True)
# initialize the inducing inputs
Xu = torch.arange(20.0) / 4.0
def plot_inducing_points(Xu, ax=None):
for xu in Xu:
g = ax.axvline(xu, color="red", linestyle="-.", alpha=0.5)
ax.legend(
handles=[g],
labels=["Inducing Point Locations"],
bbox_to_anchor=(0.5, 1.15),
loc="upper center",
)
plot_inducing_points(Xu, plt.gca())
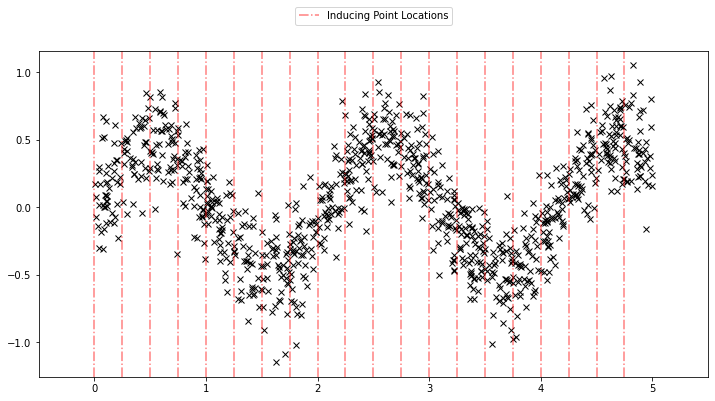
[20]:
# initialize the kernel and model
pyro.clear_param_store()
kernel = gp.kernels.RBF(input_dim=1)
# we increase the jitter for better numerical stability
sgpr = gp.models.SparseGPRegression(X, y, kernel, Xu=Xu, jitter=1.0e-5)
# the way we setup inference is similar to above
optimizer = torch.optim.Adam(sgpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
locations = []
variances = []
lengthscales = []
noises = []
num_steps = 2000 if not smoke_test else 2
for i in range(num_steps):
optimizer.zero_grad()
loss = loss_fn(sgpr.model, sgpr.guide)
locations.append(sgpr.Xu.data.numpy().copy())
variances.append(sgpr.kernel.variance.item())
noises.append(sgpr.noise.item())
lengthscales.append(sgpr.kernel.lengthscale.item())
loss.backward()
optimizer.step()
losses.append(loss.item())
[21]:
plot_loss(losses)
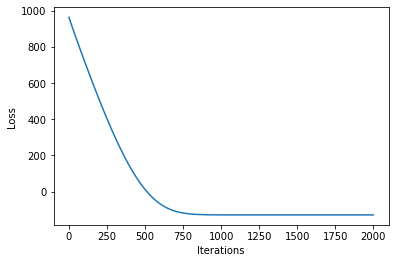
现在,我们可以绘制学习模型的预测结果以及优化后的诱导点位置。
[22]:
plot(model=sgpr, plot_observed_data=True, plot_predictions=True)
plot_inducing_points(sgpr.Xu.data.numpy(), plt.gca())
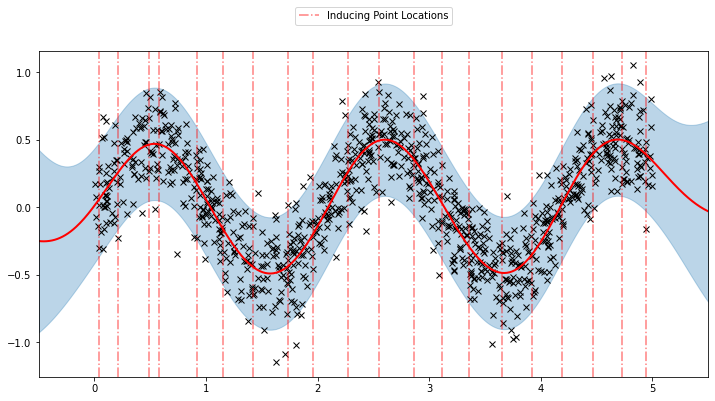
我们可以看到该模型学习到了对数据合理的拟合。我们还可以看到诱导点位置与我们的初始化有相当大的不同。我们还可以通过下面的动画查看模型学习过程。
[23]:
fig, ax = plt.subplots(figsize=(12, 6))
def update(iteration):
pyro.clear_param_store()
ax.cla()
kernel_iter = gp.kernels.RBF(
input_dim=1,
variance=torch.tensor(variances[iteration]),
lengthscale=torch.tensor(lengthscales[iteration]),
)
sgpr_iter = gp.models.SparseGPRegression(
X,
y,
kernel_iter,
Xu=torch.tensor(locations[iteration]),
noise=torch.tensor(noises[iteration]),
jitter=1.0e-5,
)
plot(model=sgpr_iter, plot_observed_data=True, plot_predictions=True, ax=ax)
plot_inducing_points(sgpr_iter.Xu.data.numpy(), ax=ax)
ax.set_title(f"Iteration: {iteration}, Loss: {losses[iteration]:0.2f}")
fig.tight_layout()
anim = FuncAnimation(fig, update, frames=np.arange(0, num_steps, 30), interval=100)
plt.close()
anim.save("../source/_static/img/svgpr-fit.gif", fps=60)

目前 Pyro 中实现了三种不同的稀疏近似方法:
“DTC” (确定性训练条件)
“FITC” (完全独立训练条件)
“VFE” (变分自由能)
默认情况下,SparseGPRegression 将使用“VFE”作为推断方法。我们可以通过向 SparseGPRegression 传递不同的 approx 标志来使用其他方法。
更多稀疏 GP¶
上面的 GPRegression 和 SparseGPRegression 都仅限于高斯似然。我们可以将其他似然用于 GP——例如,我们可以使用伯努利似然进行分类问题——但推断问题变得更加困难。在本节中,我们将展示如何使用 VariationalSparseGP 模块,该模块可以处理非高斯似然。因此,为了与我们之前所做的工作进行比较,我们仍然将使用高斯似然。重点在于底层进行的推断可以支持其他似然。
高斯似然¶
[24]:
# initialize the inducing inputs
Xu = torch.arange(10.0) / 2.0
# initialize the kernel, likelihood, and model
pyro.clear_param_store()
kernel = gp.kernels.RBF(input_dim=1)
likelihood = gp.likelihoods.Gaussian()
# turn on "whiten" flag for more stable optimization
vsgp = gp.models.VariationalSparseGP(
X, y, kernel, Xu=Xu, likelihood=likelihood, whiten=True
)
# instead of defining our own training loop, we will
# use the built-in support provided by the GP module
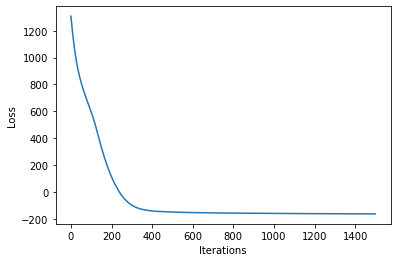
num_steps = 1500 if not smoke_test else 2
losses = gp.util.train(vsgp, num_steps=num_steps)
plot_loss(losses)
[25]:
plot(model=vsgp, plot_observed_data=True, plot_predictions=True)
GP 分类¶
现在我们将简要讨论多类分类的 GP 分类。与 GP 回归相比,模型规范需要进行的两个主要更改是
或
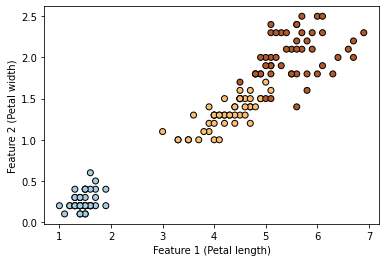
在我们的示例中,我们将使用 Iris 数据集。我们将三个类别编码为数字:0 代表 setosa,1 代表 versicolor,2 代表 virginica。此外,为了简化示例,我们将只考虑两个输入特征(花瓣长度和花瓣宽度)。
[26]:
df = sns.load_dataset("iris")
df.head()
[26]:
| 萼片长度 | 萼片宽度 | 花瓣长度 | 花瓣宽度 | 物种 | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
[27]:
# only take petal length and petal width
X = torch.from_numpy(
df[df.columns[2:4]].values.astype("float64"),
)
df["species"] = df["species"].astype("category")
# encode the species as 0, 1, 2
y = torch.from_numpy(df["species"].cat.codes.values.copy())
[28]:
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors=(0, 0, 0))
plt.xlabel("Feature 1 (Petal length)")
_ = plt.ylabel("Feature 2 (Petal width)")
[29]:
kernel = gp.kernels.RBF(input_dim=2)
pyro.clear_param_store()
likelihood = gp.likelihoods.MultiClass(num_classes=3)
# Important -- we need to add latent_shape argument here to the number of classes we have in the data
model = gp.models.VariationalGP(
X,
y,
kernel,
likelihood=likelihood,
whiten=True,
jitter=1e-03,
latent_shape=torch.Size([3]),
)
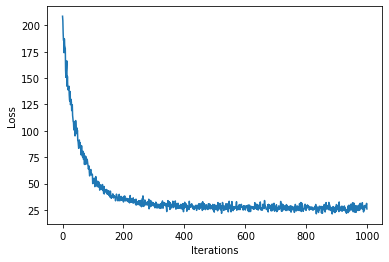
num_steps = 1000
loss = gp.util.train(model, num_steps=num_steps)
[30]:
plot_loss(loss)
[31]:
mean, var = model(X)
y_hat = model.likelihood(mean, var)
print(f"Accuracy: {(y_hat==y).sum()*100/(len(y)) :0.2f}%")
Accuracy: 96.00%
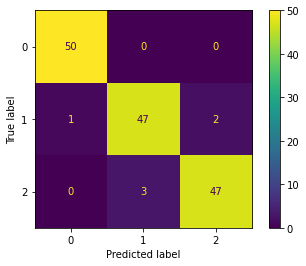
我们还可以计算混淆矩阵。
[32]:
cm = confusion_matrix(y, y_hat, labels=[0, 1, 2])
ConfusionMatrixDisplay(cm).plot()
[32]:
<sklearn.metrics._plot.confusion_matrix.ConfusionMatrixDisplay at 0x133782b80>
和之前一样,让我们在二维网格上绘制预测结果。
[33]:
xs = torch.linspace(X[:, 0].min() - 0.5, X[:, 0].max() + 0.5, steps=100)
ys = torch.linspace(X[:, 1].min() - 0.5, X[:, 1].max() + 0.5, steps=100)
xx, yy = torch.meshgrid(xs, ys, indexing="xy")
with torch.no_grad():
mean, var = model(torch.vstack((xx.ravel(), yy.ravel())).t())
Z = model.likelihood(mean, var)
[34]:
def plot_pred_2d(arr, xx, yy, contour=False, ax=None, title=None):
if ax is None:
fig, ax = plt.subplots()
image = ax.imshow(
arr,
interpolation="nearest",
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
aspect="equal",
origin="lower",
cmap=plt.cm.PuOr_r,
)
if contour:
contours = ax.contour(
xx,
yy,
torch.sigmoid(mean).reshape(xx.shape),
levels=[0.5],
linewidths=2,
colors=["k"],
)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
ax.get_figure().colorbar(image, cax=cax)
if title:
ax.set_title(title)
[35]:
fig, ax = plt.subplots(ncols=3, figsize=(16, 4))
for cl in [0, 1, 2]:
plot_pred_2d(
mean[cl, :].reshape(xx.shape), xx, yy, ax=ax[cl], title=f"f (class {cl})"
)

[36]:
p_class = torch.nn.functional.softmax(mean, dim=0)
[37]:
fig, ax = plt.subplots(ncols=3, figsize=(16, 4))
for cl in [0, 1, 2]:
plot_pred_2d(
p_class[cl, :].reshape(xx.shape), xx, yy, ax=ax[cl], title=f" p(class {cl})"
)

[38]:
plot_pred_2d(Z.reshape(xx.shape), xx, yy, title="Prediction")
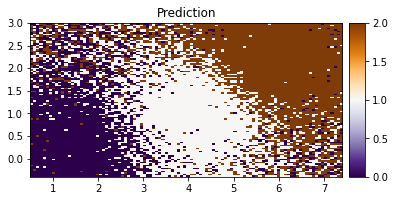
我们可以看到我们的模型在根据两个特征对 IRIS 数据进行分类方面做得很好。
核组合¶
现在我们来看看如何组合不同的核。我们将创建一个包含线性趋势和一些周期性的简单数据集。
[39]:
X = torch.linspace(-5, 5, 100)
y = torch.sin(X * 8) + 2 * X + 4 + 0.2 * torch.rand_like(X)
plt.scatter(X, y)
plt.show()

我们可以清楚地看到数据中的趋势。让我们使用如下的组合核:
线性 + RBF * 周期性
[40]:
pyro.clear_param_store()
linear = gp.kernels.Linear(
input_dim=1,
)
periodic = gp.kernels.Periodic(
input_dim=1, period=torch.tensor(0.5), lengthscale=torch.tensor(4.0)
)
rbf = gp.kernels.RBF(
input_dim=1, lengthscale=torch.tensor(0.5), variance=torch.tensor(0.5)
)
k1 = gp.kernels.Product(kern0=rbf, kern1=periodic)
k = gp.kernels.Sum(linear, k1)
model = gp.models.GPRegression(
X=X,
y=y,
kernel=k,
jitter=2e-3,
)
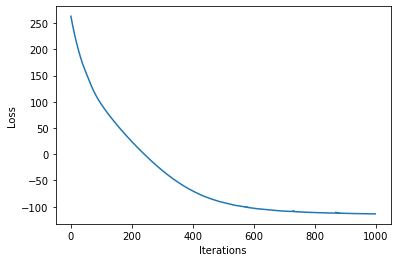
loss = gp.util.train(model)
plot_loss(loss)
[41]:
plt.scatter(X, y, s=50, alpha=0.5)
with torch.no_grad():
mean, var = model(X)
_ = plt.plot(X, mean, color="C3", lw=2)
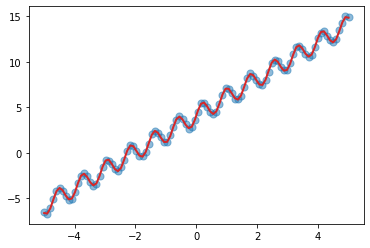
我们可以看到,我们的核组合在学习数据中固有的趋势和周期性方面做得相当不错。
这就是全部内容。有关 pyro.contrib.gp 模块的更多详细信息,请参阅文档。有关二元分类的示例,请参见此处;有关深度核学习的示例,请参见此处;有关使用深度核学习进行 GP 分类的高级示例,请参见此处。
参考¶
[1] Deep Gaussian processes and variational propagation of uncertainty, Andreas Damianou
[2] 使用幂期望传播的稀疏高斯过程逼近统一框架, Thang D. Bui, Josiah Yan, and Richard E. Turner
[3] 可扩展变分高斯过程分类, James Hensman, Alexander G. de G. Matthews, and Zoubin Ghahramani
[4] 机器学习中的高斯过程, Carl E. Rasmussen, and Christopher K. I. Williams
[5] 稀疏近似高斯过程回归的统一视角, Joaquin Quinonero-Candela, and Carl E. Rasmussen