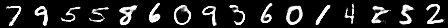带归一化流先验的变分自编码器¶
使用归一化流作为潜变量的先验,而非典型的标准高斯分布,是一种使变分自编码器 (VAE) 更具表达能力的简单方法。本 Notebook 演示了如何实现一个将归一化流作为 MNIST 数据集先验的 VAE。我们强烈建议您先阅读 Pyro 的 VAE 教程。
在本 Notebook 中,我们使用 Zuko 来实现归一化流,但使用其他基于 PyTorch 的流库也能获得类似结果。
[1]:
import pyro
import torch
import torch.nn as nn
import torch.utils.data as data
import zuko
from pyro.contrib.zuko import ZukoToPyro
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
from torch import Tensor
from torchvision.datasets import MNIST
from torchvision.transforms.functional import to_tensor, to_pil_image
from tqdm import tqdm
数据¶
MNIST 数据集包含 28 x 28 像素的灰度图像,代表手写数字(0 到 9)。
[2]:
trainset = MNIST(root='', download=True, train=True, transform=to_tensor)
trainloader = data.DataLoader(trainset, batch_size=256, shuffle=True)
[3]:
x = [trainset[i][0] for i in range(16)]
x = torch.cat(x, dim=-1)
to_pil_image(x)
[3]:

模型¶
与 之前的教程 类似,我们选择一个(对角线)高斯模型作为编码器 \(q_\psi(z | x)\) 以及伯努利模型作为解码器 \(p_\phi(x | z)\)。
[4]:
class GaussianEncoder(nn.Module):
def __init__(self, features: int, latent: int):
super().__init__()
self.hyper = nn.Sequential(
nn.Linear(features, 1024),
nn.ReLU(),
nn.Linear(1024, 1024),
nn.ReLU(),
nn.Linear(1024, 2 * latent),
)
def forward(self, x: Tensor):
phi = self.hyper(x)
mu, log_sigma = phi.chunk(2, dim=-1)
return pyro.distributions.Normal(mu, log_sigma.exp()).to_event(1)
class BernoulliDecoder(nn.Module):
def __init__(self, features: int, latent: int):
super().__init__()
self.hyper = nn.Sequential(
nn.Linear(latent, 1024),
nn.ReLU(),
nn.Linear(1024, 1024),
nn.ReLU(),
nn.Linear(1024, features),
)
def forward(self, z: Tensor):
phi = self.hyper(z)
rho = torch.sigmoid(phi)
return pyro.distributions.Bernoulli(rho).to_event(1)
然而,我们选择一个 masked autoregressive flow (MAF) 作为先验 \(p_\phi(z)\) 而非典型的标准高斯分布 \(\mathcal{N}(0, I)\)。我们没有自己实现 MAF,而是从 Zuko 库中借用。因为 Zuko 分布与 Pyro 分布非常相似,一个简单的封装器 (ZukoToPyro) 就足以让 Zuko 和 Pyro 100% 兼容。
[5]:
class VAE(nn.Module):
def __init__(self, features: int, latent: int = 16):
super().__init__()
self.encoder = GaussianEncoder(features, latent)
self.decoder = BernoulliDecoder(features, latent)
self.prior = zuko.flows.MAF(
features=latent,
transforms=3,
hidden_features=(256, 256),
)
def model(self, x: Tensor):
pyro.module("prior", self.prior)
pyro.module("decoder", self.decoder)
with pyro.plate("batch", len(x)):
z = pyro.sample("z", ZukoToPyro(self.prior()))
x = pyro.sample("x", self.decoder(z), obs=x)
def guide(self, x: Tensor):
pyro.module("encoder", self.encoder)
with pyro.plate("batch", len(x)):
z = pyro.sample("z", self.encoder(x))
vae = VAE(784, 16).cuda()
vae
[5]:
VAE(
(encoder): GaussianEncoder(
(hyper): Sequential(
(0): Linear(in_features=784, out_features=1024, bias=True)
(1): ReLU()
(2): Linear(in_features=1024, out_features=1024, bias=True)
(3): ReLU()
(4): Linear(in_features=1024, out_features=32, bias=True)
)
)
(decoder): BernoulliDecoder(
(hyper): Sequential(
(0): Linear(in_features=16, out_features=1024, bias=True)
(1): ReLU()
(2): Linear(in_features=1024, out_features=1024, bias=True)
(3): ReLU()
(4): Linear(in_features=1024, out_features=784, bias=True)
)
)
(prior): MAF(
(transform): LazyComposedTransform(
(0): MaskedAutoregressiveTransform(
(base): MonotonicAffineTransform()
(order): [0, 1, 2, 3, 4, ..., 11, 12, 13, 14, 15]
(hyper): MaskedMLP(
(0): MaskedLinear(in_features=16, out_features=256, bias=True)
(1): ReLU()
(2): MaskedLinear(in_features=256, out_features=256, bias=True)
(3): ReLU()
(4): MaskedLinear(in_features=256, out_features=32, bias=True)
)
)
(1): MaskedAutoregressiveTransform(
(base): MonotonicAffineTransform()
(order): [15, 14, 13, 12, 11, ..., 4, 3, 2, 1, 0]
(hyper): MaskedMLP(
(0): MaskedLinear(in_features=16, out_features=256, bias=True)
(1): ReLU()
(2): MaskedLinear(in_features=256, out_features=256, bias=True)
(3): ReLU()
(4): MaskedLinear(in_features=256, out_features=32, bias=True)
)
)
(2): MaskedAutoregressiveTransform(
(base): MonotonicAffineTransform()
(order): [0, 1, 2, 3, 4, ..., 11, 12, 13, 14, 15]
(hyper): MaskedMLP(
(0): MaskedLinear(in_features=16, out_features=256, bias=True)
(1): ReLU()
(2): MaskedLinear(in_features=256, out_features=256, bias=True)
(3): ReLU()
(4): MaskedLinear(in_features=256, out_features=32, bias=True)
)
)
)
(base): Unconditional(DiagNormal(loc: torch.Size([16]), scale: torch.Size([16])))
)
)
训练¶
我们使用标准的随机变分推断 (SVI) 流程来训练我们的 VAE。
[6]:
pyro.clear_param_store()
svi = SVI(vae.model, vae.guide, Adam({'lr': 1e-3}), loss=Trace_ELBO())
for epoch in (bar := tqdm(range(96))):
losses = []
for x, _ in trainloader:
x = x.round().flatten(-3).cuda()
losses.append(svi.step(x))
losses = torch.tensor(losses)
bar.set_postfix(loss=losses.sum().item() / len(trainset))
100%|██████████| 96/96 [24:04<00:00, 15.05s/it, loss=63.1]
训练完成后,我们可以通过从先验中抽样潜变量并对其进行解码来生成 MNIST 图像。
[7]:
z = vae.prior().sample((16,))
x = vae.decoder(z).mean.reshape(-1, 28, 28)
to_pil_image(x.movedim(0, 1).reshape(28, -1))
[7]: