归一化流 - 简介¶
本教程介绍 Pyro 内置的归一化流。它独立于 Pyro 的大部分内容,但用户可能希望阅读张量形状教程中关于分布形状的内容。
Pyro 内置流的开发已停止,转而支持外部库,例如 Zuko、nflows、normflows 或 FlowTorch。其中一些库的接口可能与 Pyro 不直接兼容。请参阅 使用流引导的 SVI 和 使用流先验的 VAE 教程,了解在 Pyro 中使用 Zuko 的示例用法。
简介¶
在标准概率建模实践中,我们使用简单的参数分布(如正态分布、指数分布和拉普拉斯分布)来表示我们对未知连续量的信念。然而,使用这种通常对称且单峰(或者当我们取其混合时具有固定数量的模式)的简单形式,限制了我们方法的性能和灵活性。例如,变分自编码器中的标准变分推断使用独立的单变量正态分布来表示变分族。真实的后验既不是独立的也不是正态分布的,这导致了次优的推断并简化了学习到的模型。在其他情况下,我们同样受到无法建模多峰分布以及厚尾或薄尾分布的限制。
归一化流 [1-4] 是一族用于构建灵活的可学习概率分布的方法,通常使用神经网络,这使我们能够超越简单参数形式的限制。Pyro 包含最先进的归一化流实现,本教程解释了如何使用此库学习复杂模型和执行灵活的变分推断。我们介绍了归一化流 (NFs) 的主要思想,并演示了使用逐元素、多变量和条件流学习简单的单变量分布。
单变量分布¶
背景¶
归一化流是一族用于构建灵活分布的方法。我们先将注意力限制在表示单变量分布上。基本思想是,一个简单的噪声源(例如具有标准正态分布的变量,\(X\sim\mathcal{N}(0,1)\))通过一个双射(即可逆)函数 \(g(\cdot)\) 产生一个更复杂的变换变量 \(Y=g(X)\)。
对于给定的随机变量,我们通常希望执行两个操作:采样和评分。对 \(Y\) 进行采样是微不足道的。首先,我们采样 \(X=x\),然后计算 \(y=g(x)\)。对 \(Y\) 进行评分,或者更确切地说,评估对数密度 \(\log p_Y(y)\),则更为复杂。 \(Y\) 的密度如何与 \(X\) 的密度相关?我们可以使用积分微积分的换元法则来回答这个问题。假设我们要评估函数 \(f(X)\) 的期望。那么,
\begin{align} \mathbb{E}_{p_X(\cdot)}\left[f(X)\right] &= \int_{\text{supp}(X)}f(x)p_X(x)dx\\ &= \int_{\text{supp}(Y)}f(g^{-1}(y))p_X(g^{-1}(y))\left|\frac{dx}{dy}\right|dy\\ &= \mathbb{E}_{p_Y(\cdot)}\left[f(g^{-1}(Y))\right], \end{align}
其中 \(\text{supp}(X)\) 表示 \(X\) 的支撑集,在此例中为 \((-\infty,\infty)\)。关键在于,我们利用 \(g\) 是双射的事实,将换元法则应用于从第一行到第二行的转换。将最后两行等同起来,我们得到,
\begin{align} \log p_Y(y) & = \log p_X(g^{-1}(y)) + \log\left|\frac{dx}{dy}\right| \\ & = \log p_X(g^{-1}(y)) - \log\left|\frac{dy}{dx}\right|. \end{align}
直观地说,这个等式表示 \(Y\) 的密度等于 \(X\) 中对应点的密度,再加上一个修正项,该修正项用于校正由变换引起的围绕 \(Y\) 的无穷小长度的体积变形。
如果 \(g\) 构建得很巧妙(我们很快会看到几个例子),我们可以生成比标准正态噪声更复杂的分布,并且仍然具有容易的采样和计算可处理的评分。此外,我们可以组合这样的双射变换以生成更复杂的分布。通过归纳论证,如果我们有一个由 \(L\) 个变换组成的序列 \((g_1, g_2, \ldots, g_L)\),使得 \(Y = g(X) = g_L \circ \cdots g_2 \circ g_1(X)\),则 \(Y\) 的对数密度为
\begin{align} \log p_Y(y) = \log p_X(y_0) + \sum^{L}_{l=1} \log \left| \frac{dg^{-1}_{l}(y_l)}{dy_{l}} \right| \end{align}
其中 \(y_{l} = y\) 且 \(y_{l-1} = g^{-1}_l(y_{l})\)。
在后面的章节中,我们将看到如何将此方法推广到多变量 \(X\)。归一化流领域旨在为多变量 \(X\) 构建这样的 \(g\),将简单的 i.i.d. 标准正态噪声转换为复杂、可学习的高维分布。该方法已应用于图像建模、文本转语音、无监督语言归纳、数据压缩和分子结构建模等多种应用。由于概率分布是概率建模中最基本的部分,我们很可能在不久的将来看到更多令人兴奋的最先进的应用。
Pyro 中的固定单变量变换¶
PyTorch 包含用于表示*固定*单变量双射变换以及从中派生的变换分布进行采样/评分的类。Pyro 扩展了此功能,提供了使用该领域最新发展的全面*可学习*单变量和多变量变换库。由于 Pyro 导入了所有 PyTorch 的分布和变换,我们将只使用 Pyro。我们还注意到,Pyro 中的 NF 组件可以独立于 Pyro 的概率编程功能使用,这也是我们在前两个教程中将要做的。
让我们首先展示如何表示和操作一个简单的变换分布,
\begin{align} X &\sim \mathcal{N}(0,1)\\ Y &= \text{exp}(X). \end{align}
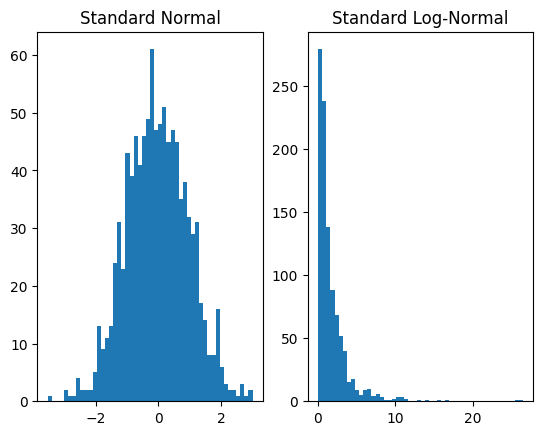
您可能已经认识到,根据定义,这是 \(Y\sim\text{LogNormal}(0,1)\)。
我们首先导入相关库
[1]:
import torch
import pyro
import pyro.distributions as dist
import pyro.distributions.transforms as T
import matplotlib.pyplot as plt
import seaborn as sns
import os
smoke_test = ('CI' in os.environ)
各种双射变换位于 pyro.distributions.transforms 模块中,而用于定义变换分布的类位于 pyro.distributions 中。我们首先创建 \(X\) 的基础分布和封装变换 \(\text{exp}(\cdot)\) 的类
[2]:
dist_x = dist.Normal(torch.zeros(1), torch.ones(1))
exp_transform = T.ExpTransform()
ExpTransform 类派生自 Transform,并定义了该变换的前向、逆向和对数绝对导数运算,
\begin{align} g(x) &= \text{exp(x)}\\ g^{-1}(y) &= \log(y)\\ \log \left|\frac{dg}{dx}\right| &= x. \end{align}
通常,一个变换类定义了这三个运算,从这些运算中就足以执行采样和评分。
TransformedDistribution 类接受一个简单噪声的基础分布和一个变换列表,并封装了通过按顺序应用这些变换形成的分布。我们使用它如下:
[3]:
dist_y = dist.TransformedDistribution(dist_x, [exp_transform])
现在,绘制两者的样本以验证我们生成了对数正态分布
[4]:
plt.subplot(1, 2, 1)
plt.hist(dist_x.sample([1000]).numpy(), bins=50)
plt.title('Standard Normal')
plt.subplot(1, 2, 2)
plt.hist(dist_y.sample([1000]).numpy(), bins=50)
plt.title('Standard Log-Normal')
plt.show()
我们的例子使用了一个单一的变换。然而,我们可以组合变换来产生更具表达力的分布。例如,如果我们应用一个仿射变换,我们可以产生一般的对数正态分布,
\begin{align} X &\sim \mathcal{N}(0,1)\\ Y &= \text{exp}(\mu+\sigma X). \end{align}
或者说,\(Y\sim\text{LogNormal}(\mu,\sigma^2)\)。在 Pyro 中,例如对于 \(\mu=3, \sigma=0.5\),这可以通过以下方式实现:
[5]:
dist_x = dist.Normal(torch.zeros(1), torch.ones(1))
affine_transform = T.AffineTransform(loc=3, scale=0.5)
exp_transform = T.ExpTransform()
dist_y = dist.TransformedDistribution(dist_x, [affine_transform, exp_transform])
plt.subplot(1, 2, 1)
plt.hist(dist_x.sample([1000]).numpy(), bins=50)
plt.title('Standard Normal')
plt.subplot(1, 2, 2)
plt.hist(dist_y.sample([1000]).numpy(), bins=50)
plt.title('Log-Normal')
plt.show()
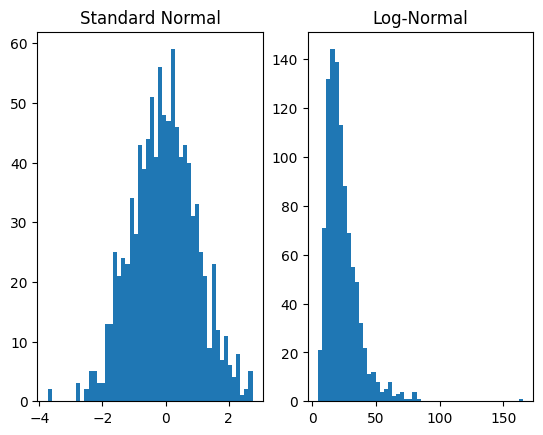
对于前向运算,变换按照 TransformedDistribution 的第二个参数列表中的顺序应用。在这种情况下,首先对基础分布应用 AffineTransform,然后应用 ExpTransform。
Pyro 中的可学习单变量分布¶
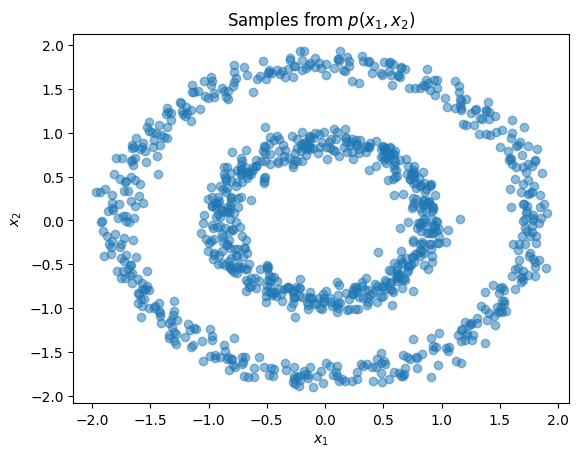
介绍完可逆变换和变换分布的接口后,我们现在展示如何表示*可学习*变换并将其用于密度估计。本节和下一节的数据集将包含沿着两个同心圆的样本。检查联合分布和边缘分布
[6]:
import numpy as np
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
n_samples = 1000
X, y = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.05)
X = StandardScaler().fit_transform(X)
plt.title(r'Samples from $p(x_1,x_2)$')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.scatter(X[:,0], X[:,1], alpha=0.5)
plt.show()
plt.subplot(1, 2, 1)
sns.distplot(X[:,0], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2})
plt.title(r'$p(x_1)$')
plt.subplot(1, 2, 2)
sns.distplot(X[:,1], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2})
plt.title(r'$p(x_2)$')
plt.show()
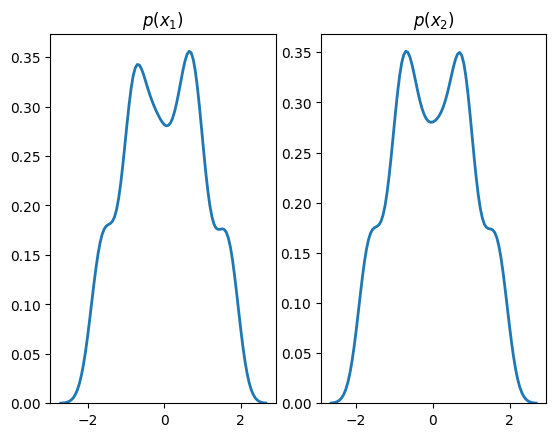
标准变换派生自 Transform 类,并且未设计为包含可学习参数。另一方面,可学习变换派生自 TransformModule,它是一个 torch.nn.Module,并向对象注册参数。
我们将使用这样的变换,Spline [5,6],在二维输入上定义,来学习上述分布的边缘分布
[7]:
base_dist = dist.Normal(torch.zeros(2), torch.ones(2))
spline_transform = T.Spline(2, count_bins=16)
flow_dist = dist.TransformedDistribution(base_dist, [spline_transform])
此变换通过一个单独的单调递增函数(称为样条曲线)处理其输入的每个维度。从高层次看,样条曲线是一个复杂的参数化曲线,我们可以为其定义特定的点(称为结),它将经过这些点,以及在结处的导数。结及其导数是可学习的参数,例如通过最大似然目标的随机梯度下降来学习,如下所示
[8]:
%%time
steps = 1 if smoke_test else 1001
dataset = torch.tensor(X, dtype=torch.float)
optimizer = torch.optim.Adam(spline_transform.parameters(), lr=1e-2)
for step in range(steps):
optimizer.zero_grad()
loss = -flow_dist.log_prob(dataset).mean()
loss.backward()
optimizer.step()
flow_dist.clear_cache()
if step % 200 == 0:
print('step: {}, loss: {}'.format(step, loss.item()))
step: 0, loss: 2.682476758956909
step: 200, loss: 1.278384804725647
step: 400, loss: 1.2647961378097534
step: 600, loss: 1.2601449489593506
step: 800, loss: 1.2561875581741333
step: 1000, loss: 1.2545257806777954
CPU times: user 4.92 s, sys: 69.3 ms, total: 4.99 s
Wall time: 5.01 s
请注意,我们在每次优化步骤后调用 flow_dist.clear_cache() 来清除变换的前向-逆向缓存。这是必需的,因为 flow_dist 的 spline_transform 是一个有状态的 TransformModule,而不是一个纯粹无状态的 Transform 对象。纯函数式 Pyro 代码通常在每次模型执行时创建 Transform 对象,然后在 .backward() 后丢弃它们,从而有效地清除变换缓存。相比之下,在本教程中,我们创建有状态的模块对象,并且需要在更新后手动清除其缓存。
学习后从变换分布中绘制样本并绘制结果
[9]:
X_flow = flow_dist.sample(torch.Size([1000,])).detach().numpy()
plt.title(r'Joint Distribution')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.scatter(X[:,0], X[:,1], label='data', alpha=0.5)
plt.scatter(X_flow[:,0], X_flow[:,1], color='firebrick', label='flow', alpha=0.5)
plt.legend()
plt.show()
plt.subplot(1, 2, 1)
sns.distplot(X[:,0], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,0], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_1)$')
plt.subplot(1, 2, 2)
sns.distplot(X[:,1], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,1], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_2)$')
plt.show()
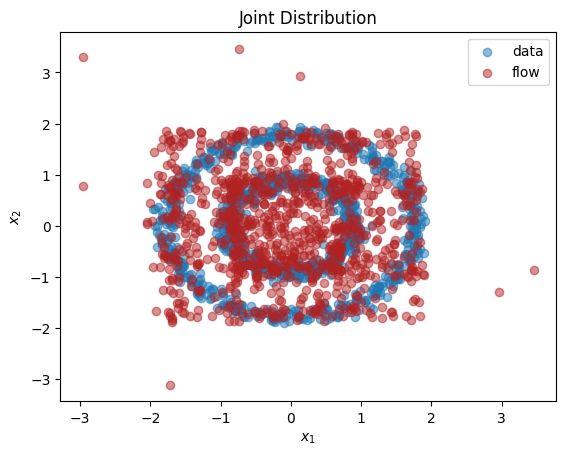
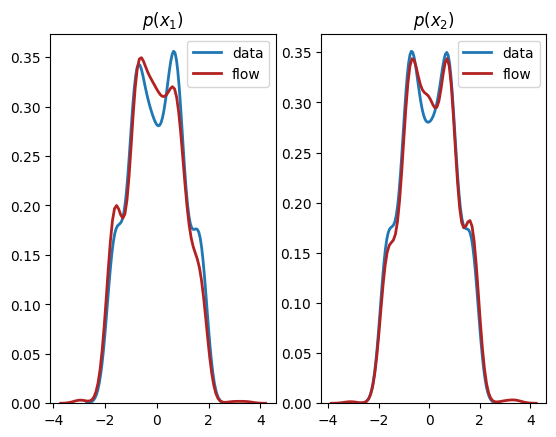
如我们所见,我们已经学习到了边缘分布 \(p(x_1),p(x_2)\) 的近似值。用标准方法(例如正态分布的混合)拟合这些不规则形状的边缘分布将是一个挑战。正如预期的那样,由于这两个维度之间存在依赖关系,我们没有学到联合分布 \(p(x_1,x_2)\) 的良好表示。在下一节中,我们将解释如何学习维度不独立的多变量分布。
多变量分布¶
背景¶
归一化流的基本思想也适用于多变量随机变量,这也是其价值所在——表示复杂的高维分布。在这种情况下,一个简单的多变量噪声源,例如标准 i.i.d. 正态分布,\(X\sim\mathcal{N}(\mathbf{0},I_{D\times D})\),通过一个向量值双射 \(g:\mathbb{R}^D\rightarrow\mathbb{R}^D\),产生更复杂的变换变量 \(Y=g(X)\)。
对 \(Y\) 进行采样同样是微不足道的,并且需要计算 \(g\) 的前向传递。我们可以使用积分微积分的多变量换元法则对 \(Y\) 进行评分,
\begin{align} \mathbb{E}_{p_X(\cdot)}\left[f(X)\right] &= \int_{\text{supp}(X)}f(\mathbf{x})p_X(\mathbf{x})d\mathbf{x}\\ &= \int_{\text{supp}(Y)}f(g^{-1}(\mathbf{y}))p_X(g^{-1}(\mathbf{y}))\left|\det\frac{d\mathbf{x}}{d\mathbf{y}}\right|d\mathbf{y}\\ &= \mathbb{E}_{p_Y(\cdot)}\left[f(g^{-1}(Y))\right], \end{align}
其中 \(\det \frac{d\mathbf{x}}{d\mathbf{y}}\) 表示 \(g^{-1}(\mathbf{y})\) 的雅可比矩阵的行列式。将后两行等同起来,我们得到,
\begin{align} \log p_Y(y) &= \log p_X(g^{-1}(y)) + \log\left|\det\frac{d\mathbf{x}}{d\mathbf{y}}\right|\\ &= \log p_X(g^{-1}(y)) - \log\left|\det\frac{d\mathbf{y}}{d\mathbf{x}}\right|. \end{align}
直观地,这个等式表示 \(Y\) 的密度等于 \(X\) 中对应点的密度,加上一个修正项,用于校正由变换引起的围绕 \(Y\) 的无穷小体积的变形。例如,在 \(2\) 维空间中,雅可比行列式的绝对值的几何解释是它表示由雅可比列向量定义的平行四边形的面积。在 \(n\) 维空间中,雅可比行列式的绝对值的几何解释是它表示由雅可比列向量定义的具有 \(n\) 条边的平行多面体的超体积(更多详情请参阅 [7] 等微积分参考资料)。
与单变量情况类似,我们可以组合这样的双射变换以产生更复杂的分布。通过归纳论证,如果我们有一个由 \(L\) 个变换组成的序列 \((g_1, g_2, \ldots, g_L)\),使得 \(Y = g(X) = g_L \circ \cdots g_2 \circ g_1(X)\),则 \(Y\) 的对数密度为
\begin{align} \log p_Y(y) = \log p_X(y_0) + \sum^{L}_{l=1} \log \left| \det \frac{dg^{-1}_{l}(y_l)}{dy_{l}} \right| \end{align}
其中 \(y_{l} = y\) 且 \(y_{l-1} = g^{-1}_l(y_{l})\)。
主要的挑战在于设计可参数化的多变量双射,它们既有封闭形式的 \(g\) 和 \(g^{-1}\) 表达式,又有计算复杂度与 \(O(D)\) 而非 \(O(D^3)\) 成比例的可计算雅可比行列式,并且可以表达一类灵活的函数。
Pyro 中的多变量变换¶
到目前为止,我们已经在 Pyro 中使用了逐元素的变换。这些变换的特征是在变换对象上设置了属性 transform.event_dim == 0。这种逐元素变换只能用于表示单变量分布和维度独立的多元分布(在变分推断中称为平均场近似)。
然而,归一化流最显著的力量在于其能够使用神经网络建模复杂的高维分布,而 Pyro 包含了几种实现这一功能的流。对向量进行操作的变换具有属性 transform.event_dim == 1,对矩阵进行操作的变换具有 transform.event_dim == 2,依此类推。通常,变换的 event_dim 属性指示变换输出中有多少依赖维度。
在本节中,我们将展示如何使用 SplineCoupling 来学习我们当前示例中的双变量玩具分布。耦合变换 [8, 9] 将输入变量分为两部分,并对后半部分应用逐元素双射,其参数是前半部分的函数。可选地,也可对前半部分应用逐元素双射。在 \(d\) 处分割输入,变换为,
\begin{align} \mathbf{y}_{1:d} &= g_\theta(\mathbf{x}_{1:d})\\ \mathbf{y}_{(d+1):D} &= h_\phi(\mathbf{x}_{(d+1):D};\mathbf{x}_{1:d}), \end{align}
其中 \(\mathbf{x}_{1:d}\) 表示输入的前 \(d\) 个元素,\(g_\theta\) 是恒等函数或带有参数 \(\theta\) 的逐元素双射,而 \(h_\phi\) 是一个逐元素双射,其参数是 \(\mathbf{x}_{1:d}\) 的函数。
这种类型的变换很容易求逆。我们对前半部分 \(\mathbf{y}_{1:d}\) 求逆,然后使用得到的 \(\mathbf{x}_{1:d}\) 来评估 \(\phi\),并对后半部分求逆,
\begin{align} \mathbf{x}_{1:d} &= g_\theta^{-1}(\mathbf{y}_{1:d})\\ \mathbf{x}_{(d+1):D} &= h_\phi^{-1}(\mathbf{y}_{(d+1):D};\mathbf{x}_{1:d}). \end{align}
对 \(g\) 和 \(h\) 的不同选择构成了不同类型的耦合变换。当两者都是单调有理样条时,变换就是 Neural Spline Flow [5,6] 的样条耦合层,在 Pyro 中由 SplineCoupling 类表示。正如参考文献所示,当我们组合一系列夹在随机置换之间的耦合层时(以便引入所有维度之间的依赖关系),我们可以建模复杂的多变量分布。
Pyro 中的大多数可学习变换都有一个相应的辅助函数,用于构建一个具有正确输出形状的变换神经网络。这个神经网络输出变换的参数,被称为超网络(hypernetwork [10])。辅助函数由相应的类名的首字母小写版本表示,通常至少输入要建模的分布的输入维度或形状。例如,与 SplineCoupling 对应的辅助函数是 spline_coupling。我们使用单个样条耦合层创建一个双变量流如下
[10]:
base_dist = dist.Normal(torch.zeros(2), torch.ones(2))
spline_transform = T.spline_coupling(2, count_bins=16)
flow_dist = dist.TransformedDistribution(base_dist, [spline_transform])
与之前类似,我们在玩具数据集上训练这个分布,并绘制结果
[11]:
%%time
steps = 1 if smoke_test else 5001
dataset = torch.tensor(X, dtype=torch.float)
optimizer = torch.optim.Adam(spline_transform.parameters(), lr=5e-3)
for step in range(steps+1):
optimizer.zero_grad()
loss = -flow_dist.log_prob(dataset).mean()
loss.backward()
optimizer.step()
flow_dist.clear_cache()
if step % 500 == 0:
print('step: {}, loss: {}'.format(step, loss.item()))
step: 0, loss: 8.446191787719727
step: 500, loss: 2.0197808742523193
step: 1000, loss: 1.794958472251892
step: 1500, loss: 1.73616361618042
step: 2000, loss: 1.7254879474639893
step: 2500, loss: 1.691617488861084
step: 3000, loss: 1.679549217224121
step: 3500, loss: 1.6967085599899292
step: 4000, loss: 1.6723777055740356
step: 4500, loss: 1.6505967378616333
step: 5000, loss: 1.8024061918258667
CPU times: user 10min 41s, sys: 14.7 s, total: 10min 56s
Wall time: 1min 39s
[12]:
X_flow = flow_dist.sample(torch.Size([1000,])).detach().numpy()
plt.title(r'Joint Distribution')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.scatter(X[:,0], X[:,1], label='data', alpha=0.5)
plt.scatter(X_flow[:,0], X_flow[:,1], color='firebrick', label='flow', alpha=0.5)
plt.legend()
plt.show()
plt.subplot(1, 2, 1)
sns.distplot(X[:,0], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,0], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_1)$')
plt.subplot(1, 2, 2)
sns.distplot(X[:,1], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,1], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_2)$')
plt.show()
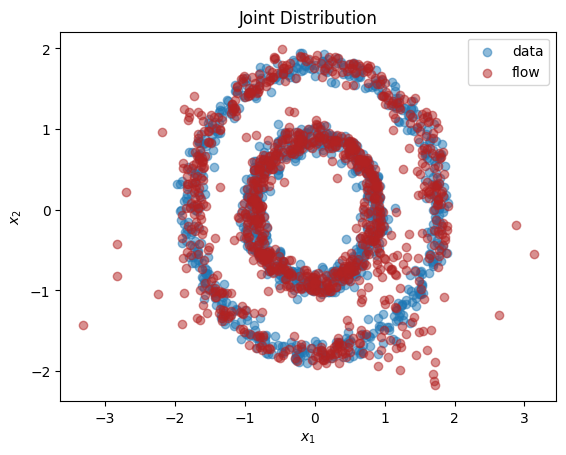
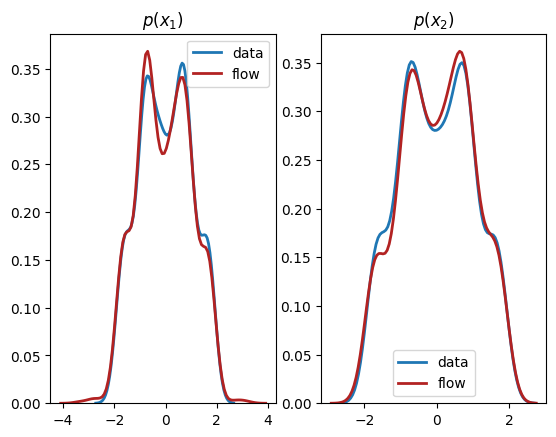
从输出中我们可以看到,这个归一化流成功地学习了单变量边缘分布*和*双变量分布。
条件分布 vs 联合分布¶
背景¶
在许多情况下,我们希望表示条件分布而不是联合分布。例如,在进行变分推断时,变分族是一类条件分布,
其中 \(\mathbf{z}\) 是潜变量,\(\mathbf{x}\) 是观测变量,希望包含一个接近模型真实后验 \(p(\mathbf{z}\mid\mathbf{x})\) 的成员。在其他情况下,我们可能希望学习生成一个对象 \(\mathbf{x}\),该对象以某些上下文 \(\mathbf{c}\) 为条件,使用 \(p_\theta(\mathbf{x}\mid\mathbf{c})\) 和观测值 \(\{(\mathbf{x}_n,\mathbf{c}_n)\}^N_{n=1}\)。例如,\(\mathbf{x}\) 可以是一个口语句子,\(\mathbf{c}\) 是一些语音特征。
归一化流理论很容易推广到条件分布。我们将条件变量表示为 \(C=\mathbf{c}\in\mathbb{R}^M\)。一个简单的多变量噪声源,例如标准 i.i.d. 正态分布,\(X\sim\mathcal{N}(\mathbf{0},I_{D\times D})\),通过一个向量值双射(也以 C 为条件)\(g:\mathbb{R}^D\times\mathbb{R}^M\rightarrow\mathbb{R}^D\),产生更复杂的变换变量 \(Y=g(X;C=\mathbf{c})\)。实际上,这通常是通过使已知归一化流双射 \(g\) 的参数成为接收 \(\mathbf{c}\) 作为输入的超网络神经网络的输出来实现的。
条件变换的采样仅仅涉及评估 \(Y=g(X; C=\mathbf{c})\)。以 \(\mathbf{c}\) 为条件进行双射,评分公式与多变量联合分布相同。
Pyro 中的条件变换¶
在 Pyro 中,大多数可学习变换都有一个相应的条件版本,该版本派生自 ConditionalTransformModule。例如,样条变换的条件版本是 ConditionalSpline,其辅助函数是 conditional_spline。
在本节中,我们将展示如何将我们的玩具数据集学习为条件分布和单变量分布乘积的分解形式,
首先,我们创建 \(x_1\) 的单变量分布,如前所示,
[13]:
dist_base = dist.Normal(torch.zeros(1), torch.ones(1))
x1_transform = T.spline(1)
dist_x1 = dist.TransformedDistribution(dist_base, [x1_transform])
通过将基础分布以及条件和非条件变换列表传递给 ConditionalTransformedDistribution 类,可以创建一个条件变换分布
[14]:
x2_transform = T.conditional_spline(1, context_dim=1)
dist_x2_given_x1 = dist.ConditionalTransformedDistribution(dist_base, [x2_transform])
您会注意到,我们将上下文变量的维度,\(M=1\),传递给了条件样条辅助函数。
在我们以 \(x_1\) 的值为条件之前,ConditionalTransformedDistribution 对象仅仅是一个占位符,不能用于采样或评分。通过调用其 .condition(context) 方法,我们获得了一个 TransformedDistribution,其中所有条件变换都已以 context 为条件。
例如,要从 \(x_2\mid x_1=1\) 中抽取一个样本
[15]:
x1 = torch.ones(1)
print(dist_x2_given_x1.condition(x1).sample())
tensor([-0.4529])
通常,上下文变量可能具有批量维度,并且这些维度必须在输入变量的批量维度上广播。
现在,结合这两个分布,并在玩具数据集上进行训练
[16]:
%%time
steps = 1 if smoke_test else 5001
modules = torch.nn.ModuleList([x1_transform, x2_transform])
optimizer = torch.optim.Adam(modules.parameters(), lr=3e-3)
x1 = dataset[:,0][:,None]
x2 = dataset[:,1][:,None]
for step in range(steps):
optimizer.zero_grad()
ln_p_x1 = dist_x1.log_prob(x1)
ln_p_x2_given_x1 = dist_x2_given_x1.condition(x1.detach()).log_prob(x2.detach())
loss = -(ln_p_x1 + ln_p_x2_given_x1).mean()
loss.backward()
optimizer.step()
dist_x1.clear_cache()
dist_x2_given_x1.clear_cache()
if step % 500 == 0:
print('step: {}, loss: {}'.format(step, loss.item()))
step: 0, loss: 5.663331031799316
step: 500, loss: 2.040316581726074
step: 1000, loss: 1.9603266716003418
step: 1500, loss: 1.8922736644744873
step: 2000, loss: 1.8509924411773682
step: 2500, loss: 1.8328033685684204
step: 3000, loss: 1.9166260957717896
step: 3500, loss: 1.877435326576233
step: 4000, loss: 1.8416743278503418
step: 4500, loss: 1.8379391431808472
step: 5000, loss: 1.824593424797058
CPU times: user 9min 24s, sys: 5.93 s, total: 9min 30s
Wall time: 1min 23s
[17]:
X = torch.cat((x1, x2), dim=-1)
x1_flow = dist_x1.sample(torch.Size([1000,]))
x2_flow = dist_x2_given_x1.condition(x1_flow).sample(torch.Size([1000,]))
X_flow = torch.cat((x1_flow, x2_flow), dim=-1)
plt.title(r'Joint Distribution')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.scatter(X[:,0], X[:,1], label='data', alpha=0.5)
plt.scatter(X_flow[:,0], X_flow[:,1], color='firebrick', label='flow', alpha=0.5)
plt.legend()
plt.show()
plt.subplot(1, 2, 1)
sns.distplot(X[:,0], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,0], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_1)$')
plt.subplot(1, 2, 2)
sns.distplot(X[:,1], hist=False, kde=True,
bins=None,
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='data')
sns.distplot(X_flow[:,1], hist=False, kde=True,
bins=None, color='firebrick',
hist_kws={'edgecolor':'black'},
kde_kws={'linewidth': 2},
label='flow')
plt.title(r'$p(x_2)$')
plt.show()
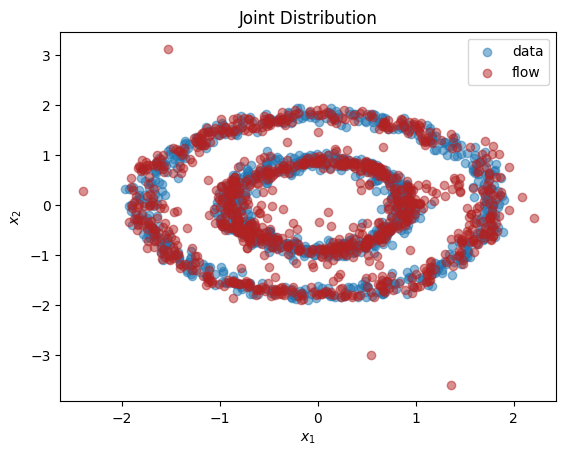
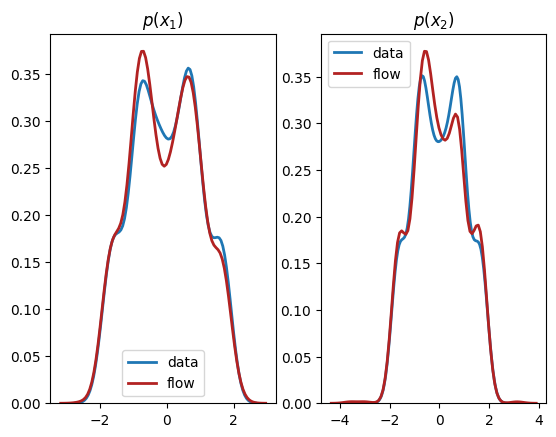
结论¶
在本教程中,我们解释了归一化流的基本思想以及 Pyro 中创建用于表示单变量、多变量和条件分布的流的接口。将流视为概率建模工具箱中强大的通用工具非常有用,您可以用它替换模型中任何现有的分布,以增加其灵活性和性能。希望您在探索归一化流的力量时玩得开心!
参考文献¶
E.G. Tabak, Christina Turner. 一族非参数密度估计算法。Communications on Pure and Applied Mathematics, 66(2):145–164, 2013。
Danilo Jimenez Rezende, Shakir Mohamed. 变分推断与归一化流。ICML 2015。
Ivan Kobyzev, Simon J.D. Prince, and Marcus A. Brubaker. 归一化流:简介与现有方法综述。[arXiv:1908.09257] 2019。
George Papamakarios, Eric Nalisnick, Danilo Jimenez Rezende, Shakir Mohamed, Balaji Lakshminarayanan. 用于概率建模和推断的归一化流。[arXiv:1912.02762] 2019。
Conor Durkan, Artur Bekasov, Iain Murray, George Papamakarios. 神经样条流。NeurIPS 2019。
Hadi M. Dolatabadi, Sarah Erfani, Christopher Leckie. 使用线性有理样条的可逆生成建模。AISTATS 2020。
James Stewart. 微积分。Cengage Learning. 第9版 2020。
Laurent Dinh, David Krueger, Yoshua Bengio. NICE: 非线性独立分量估计。ICLR 2015 研讨会贡献。
Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio. 使用 Real-NVP 进行密度估计。ICLR 2017 会议论文。
David Ha, Andrew Dai, Quoc V. Le. 超网络。ICLR 2017 研讨会贡献。