(已弃用) Pyro 中的推理入门

警告

这个教程已被废弃 取而代之的是更新后的 Pyro 入门。未来可能会被删除。

许多现代机器学习任务可以视为近似推理，并可以用像 Pyro 这样的语言简洁地表达。为了引出本教程的其余部分，让我们为一个简单的物理问题构建一个生成模型，以便我们可以使用 Pyro 的推理机制来解决它。不过，我们首先需要导入本教程所需的模块。

import matplotlib.pyplot as plt
import numpy as np
import torch

import pyro
import pyro.infer
import pyro.optim
import pyro.distributions as dist

pyro.set_rng_seed(101)

一个简单示例

假设我们正在尝试弄清楚某物有多重，但我们使用的秤不可靠，每次称量同一物体时都会给出略微不同的结果。我们可以尝试通过将嘈杂的测量信息与基于对物体的一些先验知识（例如其密度或材料属性）的猜测相结合来补偿这种变异性。以下模型编码了此过程：

\[{\sf weight} \, | \, {\sf guess} \sim \cal {\sf Normal}({\sf guess}, 1)\]

\[{\sf measurement} \, | \, {\sf guess}, {\sf weight} \sim {\sf Normal}({\sf weight}, 0.75)\]

请注意，这不仅是关于我们对重量信念的模型，也是关于对其进行测量的结果的模型。该模型对应于以下随机函数：

def scale(guess):
    weight = pyro.sample("weight", dist.Normal(guess, 1.0))
    return pyro.sample("measurement", dist.Normal(weight, 0.75))

条件化

概率编程的真正用处在于能够根据观测数据对生成模型进行条件化，并推断可能产生这些数据的潜在因素。在 Pyro 中，我们将条件化的表达与其通过推理进行的评估分离开来，从而可以一次编写模型并在许多不同的观测上进行条件化。Pyro 支持将模型的内部 sample 语句约束为等于给定的一组观测值。

再次考虑 scale。假设我们想从给定输入 guess = 8.5 的 weight 分布中进行采样，但现在我们观测到 measurement == 9.5。也就是说，我们希望推断以下分布：

\[({\sf weight} \, | \, {\sf guess}, {\sf measurement} = 9.5) \sim \, ?\]

Pyro 提供了函数 pyro.condition，允许我们约束采样语句的值。pyro.condition 是一个高阶函数，它接受一个模型和一个观测字典，并返回一个新模型，该模型具有相同的输入和输出签名，但在观测到的 sample 语句处总是使用给定的值。

conditioned_scale = pyro.condition(scale, data={"measurement": torch.tensor(9.5)})

因为它就像一个普通的 Python 函数一样运行，条件化可以使用 Python 的 lambda 或 def 进行延迟或参数化。

def deferred_conditioned_scale(measurement, guess):
    return pyro.condition(scale, data={"measurement": measurement})(guess)

在某些情况下，直接将观测值传递给单个 pyro.sample 语句可能比使用 pyro.condition 更方便。pyro.sample 保留了可选的关键字参数 obs 用于此目的。

def scale_obs(guess):  # equivalent to conditioned_scale above
    weight = pyro.sample("weight", dist.Normal(guess, 1.))
    # here we condition on measurement == 9.5
    return pyro.sample("measurement", dist.Normal(weight, 0.75), obs=torch.tensor(9.5))

最后，除了用于纳入观测值的 pyro.condition 外，Pyro 还包含 pyro.do，这是 Pearl 的 do 算子的一个实现，用于因果推理，其接口与 pyro.condition 完全相同。condition 和 do 可以自由混合和组合，这使得 Pyro 成为基于模型的因果推理的强大工具。

使用 Guide 函数的灵活近似推理

让我们回到 conditioned_scale。既然我们已经在 measurement 的一个观测值上进行了条件化，我们可以使用 Pyro 的近似推理算法来估计给定 guess 和 measurement == data 时 weight 的分布。

Pyro 中的推理算法，例如 pyro.infer.SVI，允许我们使用任意随机函数，我们将称之为 guide functions 或 guides，作为近似后验分布。Guide 函数必须满足以下两个标准才能成为特定模型的有效近似：1. 模型中出现的所有未观测（即未条件化）的采样语句都出现在 guide 中。2. guide 具有与模型相同的输入签名（即接受相同的参数）。

Guide 函数可以作为可编程的、依赖于数据的提议分布，用于重要性采样、拒绝采样、序贯蒙特卡洛、MCMC 和独立 Metropolis-Hastings，也可以作为随机变分推理的变分分布或推理网络。目前，Pyro 中实现了重要性采样、MCMC 和随机变分推理，我们计划未来添加其他算法。

尽管 guide 在不同推理算法中的确切含义不同，但 guide 函数通常应选择为，原则上，其足够灵活，可以密切近似模型中所有未观测的 sample 语句的分布。

对于 scale 的情况，事实证明，给定 guess 和 measurement 时，weight 的真实后验分布实际上是 \({\sf Normal}(9.14, 0.6)\)。由于模型非常简单，我们能够解析地确定我们感兴趣的后验分布（推导过程参见例如这些笔记的 3.4 节）。

def perfect_guide(guess):
    loc = (0.75**2 * guess + 9.5) / (1 + 0.75**2)  # 9.14
    scale = np.sqrt(0.75**2 / (1 + 0.75**2))  # 0.6
    return pyro.sample("weight", dist.Normal(loc, scale))

参数化随机函数和变分推理

尽管我们可以写出 scale 的精确后验分布，但一般来说，很难指定一个能很好地近似任意条件化随机函数的后验分布的 guide。事实上，对于能够精确确定真实后验分布的随机函数来说，是例外而不是普遍情况。例如，即使是我们的 scale 示例中，如果在中间加入一个非线性函数，也可能变得难以处理。

def intractable_scale(guess):
    weight = pyro.sample("weight", dist.Normal(guess, 1.0))
    return pyro.sample("measurement", dist.Normal(some_nonlinear_function(weight), 0.75))

我们能做的是使用顶层函数 pyro.param 来指定一个由命名参数索引的 guide 族，并根据某个损失函数寻找该族中最佳近似的成员。这种近似后验推理的方法称为变分推理。

pyro.param 是 Pyro 键值参数存储的前端，这在文档中有更详细的描述。与 pyro.sample 一样，pyro.param 总是将名称作为第一个参数调用。第一次调用 pyro.param 并指定特定名称时，它会将参数存储在参数存储中并返回该值。之后，当用该名称调用时，它将返回参数存储中的值，而忽略其他任何参数。这类似于这里的 simple_param_store.setdefault，但增加了一些额外的跟踪和管理功能。

simple_param_store = {}
a = simple_param_store.setdefault("a", torch.randn(1))

例如，我们可以在 scale_posterior_guide 中对 a 和 b 进行参数化，而不是手动指定它们：

def scale_parametrized_guide(guess):
    a = pyro.param("a", torch.tensor(guess))
    b = pyro.param("b", torch.tensor(1.))
    return pyro.sample("weight", dist.Normal(a, torch.abs(b)))

顺便提一下，请注意在 scale_parametrized_guide 中，我们必须对参数 b 应用 torch.abs，因为正态分布的标准差必须是正数；类似的限制也适用于许多其他分布的参数。Pyro 基于 PyTorch 构建，其 distributions 库包含一个用于强制执行此类限制的约束模块，将约束应用于 Pyro 参数就像将相关的 constraint 对象传递给 pyro.param 一样简单。

from torch.distributions import constraints

def scale_parametrized_guide_constrained(guess):
    a = pyro.param("a", torch.tensor(guess))
    b = pyro.param("b", torch.tensor(1.), constraint=constraints.positive)
    return pyro.sample("weight", dist.Normal(a, b))  # no more torch.abs

Pyro 的构建旨在实现随机变分推理，这是一类强大且广泛适用的变分推理算法，具有三个关键特征：

1. 参数始终是实值张量

2. 我们根据模型和 guide 执行历史的样本计算损失函数的蒙特卡洛估计

3. 我们使用随机梯度下降来寻找最优参数。

将随机梯度下降与 PyTorch 的 GPU 加速张量计算和自动微分相结合，使我们能够将变分推理扩展到非常高维的参数空间和海量数据集。

Pyro 的 SVI 功能在SVI 教程中进行了详细描述。这里有一个将它应用于 scale 的非常简单的示例：

guess = 8.5

pyro.clear_param_store()
svi = pyro.infer.SVI(model=conditioned_scale,
                     guide=scale_parametrized_guide,
                     optim=pyro.optim.Adam({"lr": 0.003}),
                     loss=pyro.infer.Trace_ELBO())


losses, a, b = [], [], []
num_steps = 2500
for t in range(num_steps):
    losses.append(svi.step(guess))
    a.append(pyro.param("a").item())
    b.append(pyro.param("b").item())

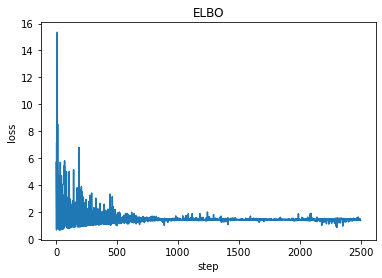
plt.plot(losses)
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
print('a = ',pyro.param("a").item())
print('b = ', pyro.param("b").item())

a =  9.11483097076416
b =  0.6279532313346863

plt.subplot(1,2,1)
plt.plot([0,num_steps],[9.14,9.14], 'k:')
plt.plot(a)
plt.ylabel('a')

plt.subplot(1,2,2)
plt.ylabel('b')
plt.plot([0,num_steps],[0.6,0.6], 'k:')
plt.plot(b)
plt.tight_layout()

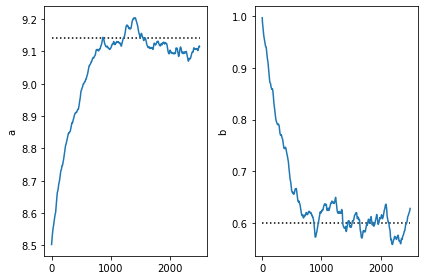
请注意，SVI 获得的参数非常接近所需条件分布的真实参数。这是预期的，因为我们的 guide 来自同一族。

请注意，优化会更新参数存储中 guide 参数的值，因此一旦我们找到好的参数值，就可以使用 guide 的样本作为下游任务的后验样本。

下一步

在变分自编码器教程中，我们将看到如何将像 scale 这样的模型用深度神经网络进行增强，并使用随机变分推理来构建图像的生成模型。