Attend Infer Repeat¶
在本教程中,我们将实现 “Attend, Infer, Repeat: Fast Scene Understanding with Generative Models” (AIR) [1] 中描述的模型和推断策略,并将其应用于 multi-mnist 数据集。
还有一个独立实现可用。
[1]:
%pylab inline
import os
from collections import namedtuple
import pyro
import pyro.optim as optim
from pyro.infer import SVI, TraceGraph_ELBO
import pyro.distributions as dist
import pyro.poutine as poutine
import pyro.contrib.examples.multi_mnist as multi_mnist
import torch
import torch.nn as nn
from torch.nn.functional import relu, sigmoid, softplus, grid_sample, affine_grid
import numpy as np
smoke_test = ('CI' in os.environ)
assert pyro.__version__.startswith('1.9.1')
Populating the interactive namespace from numpy and matplotlib
简介¶
[1] 中描述的模型是一个场景的生成模型。在本教程中,我们将使用它来建模与 [1] 中 multi-mnist 数据集相似的数据集中的图像。以下是该数据集中的一些数据点
[2]:
inpath = '../../examples/air/.data'
X_np, _ = multi_mnist.load(inpath)
X_np = X_np.astype(np.float32)
X_np /= 255.0
mnist = torch.from_numpy(X_np)
def show_images(imgs):
figure(figsize=(8, 2))
for i, img in enumerate(imgs):
subplot(1, len(imgs), i + 1)
axis('off')
imshow(img.data.numpy(), cmap='gray')
show_images(mnist[9:14])
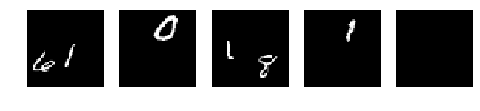
为了了解后续内容,我们首先简要概述模型和我们将采用的推理方法。我们将尽可能密切地遵循[1]中使用的命名约定。
为了了解我们将要达到的目标,我们首先简要概述模型和我们将采取的推断方法。我们将尽可能遵循 [1] 中使用的命名约定。
AIR 将生成图像的过程分解为离散的步骤,每个步骤只生成图像的一部分。更具体地说,在每个步骤中,模型将通过神经网络将一个隐“代码”变量 (z_what) 转换为一个小的图像 (y_att)。我们将这些小图像称为“对象”。在 AIR 应用于 multi-mnist 数据集的情况下,我们期望每个对象代表一个数字。模型还包括关于每个对象位置和大小的不确定性。我们将对象的位置和大小描述为它的“姿态” (z_where)。为了生成最终图像,首先将每个对象使用姿态信息 z_where 定位到更大的图像 (y) 中。最后,将所有时间步的 y 相加组合,生成最终图像 x。
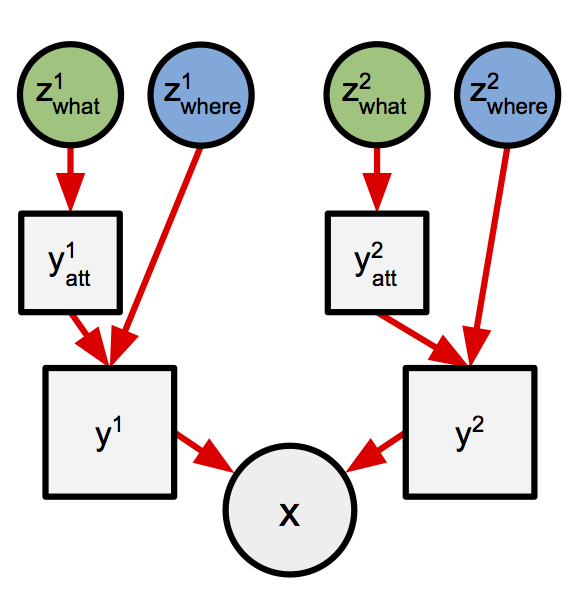
图 1:生成过程的两个步骤。
该模型使用摊销随机变分推断 (SVI) 进行推断。神经网络的参数也在推断过程中进行优化。在这种丰富的模型中进行推断总是困难的,但离散选择(本例中的步数)的存在使得该模型中的推断尤为棘手。因此,作者使用了一种称为数据依赖基线的技术来获得良好性能。这项技术可以在 Pyro 中实现,我们将在本教程后面看到如何实现。
模型¶
生成单个对象¶
让我们更仔细地看看模型。模型的核心是单个对象的生成过程。回想一下
在每个步骤中生成一个对象。
每个对象都是通过将其隐代码传递给神经网络而生成的。
我们对用于生成每个对象的隐代码及其姿态保持不确定性。
[3]:
# Create the neural network. This takes a latent code, z_what, to pixel intensities.
class Decoder(nn.Module):
def __init__(self):
super().__init__()
self.l1 = nn.Linear(50, 200)
self.l2 = nn.Linear(200, 400)
def forward(self, z_what):
h = relu(self.l1(z_what))
return sigmoid(self.l2(h))
decode = Decoder()
z_where_prior_loc = torch.tensor([3., 0., 0.])
z_where_prior_scale = torch.tensor([0.1, 1., 1.])
z_what_prior_loc = torch.zeros(50)
z_what_prior_scale = torch.ones(50)
def prior_step_sketch(t):
# Sample object pose. This is a 3-dimensional vector representing x,y position and size.
z_where = pyro.sample('z_where_{}'.format(t),
dist.Normal(z_where_prior_loc.expand(1, -1),
z_where_prior_scale.expand(1, -1))
.to_event(1))
# Sample object code. This is a 50-dimensional vector.
z_what = pyro.sample('z_what_{}'.format(t),
dist.Normal(z_what_prior_loc.expand(1, -1),
z_what_prior_scale.expand(1, -1))
.to_event(1))
# Map code to pixel space using the neural network.
y_att = decode(z_what)
# Position/scale object within larger image.
y = object_to_image(z_where, y_att)
return y
这可以在 Pyro 中如下表达
希望到目前为止,在模型中使用 pyro.sample 和 PyTorch 网络对您来说是熟悉的。如果不熟悉,您可能需要回顾一下VAE 教程。需要注意的是,我们在传递给 pyro.sample 的名称中包含了当前步骤 t,以确保名称在不同步骤中是唯一的。
函数 object_to_image 是此模型特有的,值得进一步关注。回想一下,神经网络(此处为 decode)将输出一个小图像,我们希望在执行任何必要的平移和缩放以达到 z_where 描述的姿态(位置和大小)后,将其添加到输出图像中。如何做到这一点尚不清楚,尤其不明显的是,这是否可以以保留模型可微性的方式实现,而这是我们执行SVI所必需的。然而,事实证明我们可以使用空间变换网络 (STN) [2] 来实现这一点。
[4]:
def expand_z_where(z_where):
# Takes 3-dimensional vectors, and massages them into 2x3 matrices with elements like so:
# [s,x,y] -> [[s,0,x],
# [0,s,y]]
n = z_where.size(0)
expansion_indices = torch.LongTensor([1, 0, 2, 0, 1, 3])
out = torch.cat((torch.zeros([1, 1]).expand(n, 1), z_where), 1)
return torch.index_select(out, 1, expansion_indices).view(n, 2, 3)
def object_to_image(z_where, obj):
n = obj.size(0)
theta = expand_z_where(z_where)
grid = affine_grid(theta, torch.Size((n, 1, 50, 50)))
out = grid_sample(obj.view(n, 1, 20, 20), grid)
return out.view(n, 50, 50)
对我们来说幸运的是,PyTorch 使用其 grid_sample 和 affine_grid 函数使得实现 STN 变得容易。 object_to_image 是一个简单的函数,调用这些函数,并做一些额外的工作来将 z_where 整理成预期格式。
STN 的详细讨论超出了本教程的范围。然而,就我们的目的而言,只需记住 object_to_image 将神经网络生成的小图像按照所需姿态放置到更大的图像中即可。
[5]:
pyro.set_rng_seed(0)
samples = [prior_step_sketch(0)[0] for _ in range(5)]
show_images(samples)

让我们将 prior_step_sketch 调用几次的结果可视化以阐明这一点
生成整个图像¶
[6]:
pyro.set_rng_seed(0)
def geom(num_trials=0):
p = torch.tensor([0.5])
x = pyro.sample('x{}'.format(num_trials), dist.Bernoulli(p))
if x[0] == 1:
return num_trials
else:
return geom(num_trials + 1)
# Generate some samples.
for _ in range(5):
print('sampled {}'.format(geom()))
sampled 2
sampled 3
sampled 0
sampled 1
sampled 0
完成单个步骤的实现后,接下来考虑如何使用它来生成整个图像。回想一下,我们希望对用于生成每个数据点的步数保持不确定性。关于步数的先验,我们可以选择几何分布,它可以表达如下
这是几何分布定义的直接翻译,即在伯努利试验系列中成功之前失败的次数。在这里,我们将其表示为一个递归函数,传递一个代表试验次数 num_trials 的计数器。该函数从伯努利分布中采样,如果 x == 1(表示成功),则返回 num_trials,否则进行递归调用,增加计数器。
[7]:
def geom_prior(x, step=0):
p = torch.tensor([0.5])
i = pyro.sample('i{}'.format(step), dist.Bernoulli(p))
if i[0] == 1:
return x
else:
x = x + prior_step_sketch(step)
return geom_prior(x, step + 1)
使用几何先验很有吸引力,因为它先验地不限制模型可以使用的步数。它也很方便,因为通过扩展 geometric 在每次递归调用之前生成一个对象,我们就将其从计数上的几何分布转变为步数呈几何分布的图像分布。
[8]:
pyro.set_rng_seed(4)
x_empty = torch.zeros(1, 50, 50)
samples = [geom_prior(x_empty)[0] for _ in range(5)]
show_images(samples)

让我们将此分布的一些样本可视化
旁白:向量化小批量¶
在最终实现中,我们希望并行生成样本的小批量以提高效率。虽然 Pyro 支持使用 plate 进行向量化小批量处理,但它当前要求 plate 内的每个 sample 语句为小批量中的所有样本做出选择。换句话说,小批量中的每个样本将遇到相同的 sample 语句集。这对我们来说是个问题,因为正如我们刚刚看到的,在我们的模型下,样本可以做出不同数量的选择。
解决这个问题的一种方法是让所有样本采取相同数量的步骤,但(尽可能地)抵消样本在概念上“完成”后做出的多余随机选择的影响。我们将说,一旦从伯努利随机选择中采样到零,样本就“完成”了;在此之前,我们将说样本是“活跃的”。
这第一部分很简单。参照 [1],我们选择让每个样本采取固定数量的步骤。(这样做,我们不再指定步数的几何分布,因为步数现在是有限的。探索批量中每个样本都采取步骤直到各自的伯努利试验成功为止的替代方案将很有趣,因为这将保留几何先验。)
为了解决第二部分问题,我们将采取以下步骤
仅当样本处于活跃状态时才将对象添加到输出中。
将已完成样本的随机选择的对数概率设置为零。(由于SVI 损失是对数概率的加权和,将某个选择的对数概率设置为零有效地消除了其对损失的贡献。)这可以通过使用分布的 mask() 方法来实现。
(展望未来,当我们在本教程后面实现引导网络并添加基线时,需要采取类似的措施。)
当然,我们无法撤销的一件事是执行不必要采样所做的工作。尽管如此,即使这种方法执行冗余计算,使用小批量的收益是如此之大,以至于这仍然是一个整体上的优势。
这是一个实现这些思想的更新模型步骤函数。总而言之,与
prior_step_sketch的变化如下我们添加了一个新参数
n,用于指定小批量的大小。我们现在根据从伯努利分布中采样到的值有条件地将对象添加到输出图像中。
[9]:
def prior_step(n, t, prev_x, prev_z_pres):
# Sample variable indicating whether to add this object to the output.
# We multiply the success probability of 0.5 by the value sampled for this
# choice in the previous step. By doing so we add objects to the output until
# the first 0 is sampled, after which we add no further objects.
z_pres = pyro.sample('z_pres_{}'.format(t),
dist.Bernoulli(0.5 * prev_z_pres)
.to_event(1))
z_where = pyro.sample('z_where_{}'.format(t),
dist.Normal(z_where_prior_loc.expand(n, -1),
z_where_prior_scale.expand(n, -1))
.mask(z_pres)
.to_event(1))
z_what = pyro.sample('z_what_{}'.format(t),
dist.Normal(z_what_prior_loc.expand(n, -1),
z_what_prior_scale.expand(n, -1))
.mask(z_pres)
.to_event(1))
y_att = decode(z_what)
y = object_to_image(z_where, y_att)
# Combine the image generated at this step with the image so far.
x = prev_x + y * z_pres.view(-1, 1, 1)
return x, z_pres
我们使用 mask() 将已完成样本所做随机选择的对数概率置零。
[10]:
def prior(n):
x = torch.zeros(n, 50, 50)
z_pres = torch.ones(n, 1)
for t in range(3):
x, z_pres = prior_step(n, t, x, z_pres)
return x
通过迭代此步骤函数,我们可以生成由多个对象组成的整个图像。由于 multi-mnist 数据集中的每张图像包含零个、一个或两个数字,我们将允许模型最多使用(包括)三个步骤。通过这种方式,我们确保推断必须避免使用一个或多个步骤才能正确计算输入中的对象数量。
[11]:
pyro.set_rng_seed(121)
show_images(prior(5))

我们现在已经完全指定了模型的先验。让我们可视化一些样本来感受一下这个分布
指定似然¶
为了完成模型规范,我们需要的最后一件事是似然函数。参照 [1],我们将使用固定标准差为 0.3 的高斯似然。这很容易使用 pyro.sample 的 obs 参数来实现。
[12]:
def model(data):
# Register network for optimization.
pyro.module("decode", decode)
with pyro.plate('data', data.size(0)) as indices:
batch = data[indices]
x = prior(batch.size(0)).view(-1, 50 * 50)
sd = (0.3 * torch.ones(1)).expand_as(x)
pyro.sample('obs', dist.Normal(x, sd).to_event(1),
obs=batch)
当我们稍后进行推断时,我们会发现将先验和似然打包成一个函数很方便。这也是引入 plate 的一个方便之处,我们使用它来实现数据子采样,并用 pyro.module 注册我们希望优化的网络。
引导网络¶
参照 [1],我们将在此模型中执行摊销随机变分推断。Pyro 提供了实现这种推断策略大部分功能的通用机制,但正如我们在之前的教程中看到的,我们需要提供一个模型特定的引导网络。我们在 Pyro 中称为引导网络(guide)的实体,正是论文中称为“推断网络”(inference network)的实体。
我们将围绕一个循环网络构建引导网络,以便引导网络能够捕获我们在真实后验中期望存在的(部分)依赖关系。在每个步骤中,循环网络将生成该步骤中做出的选择的参数。采样的值将被反馈到循环网络中,以便在计算下一步的参数时可以使用这些信息。深度马尔可夫模型的引导网络也具有类似的结构。
[13]:
def guide_step_basic(t, data, prev):
# The RNN takes the images and choices from the previous step as input.
rnn_input = torch.cat((data, prev.z_where, prev.z_what, prev.z_pres), 1)
h, c = rnn(rnn_input, (prev.h, prev.c))
# Compute parameters for all choices made this step, by passing
# the RNN hidden state through another neural network.
z_pres_p, z_where_loc, z_where_scale, z_what_loc, z_what_scale = predict_basic(h)
z_pres = pyro.sample('z_pres_{}'.format(t),
dist.Bernoulli(z_pres_p * prev.z_pres))
z_where = pyro.sample('z_where_{}'.format(t),
dist.Normal(z_where_loc, z_where_scale))
z_what = pyro.sample('z_what_{}'.format(t),
dist.Normal(z_what_loc, z_what_scale))
return # values for next step
与模型一样,引导网络的核心是单个步骤的逻辑。以下是其实现的草图
这将是一个可用于此模型的合理引导网络,但论文描述了一个我们可以对上述代码进行的改进。回想一下,引导网络将在每个步骤输出关于对象姿态及其隐代码的信息。我们可以进行的改进基于以下观察:一旦我们推断出对象的姿态,如果我们使用姿态信息从输入图像中裁剪出对象,并将结果(我们称之为“窗口”)通过一个附加网络来计算隐代码的参数,我们就可以更好地推断其隐代码。我们将这个附加网络称为下面的“编码器”。
[14]:
rnn = nn.LSTMCell(2554, 256)
# Takes pixel intensities of the attention window to parameters (mean,
# standard deviation) of the distribution over the latent code,
# z_what.
class Encoder(nn.Module):
def __init__(self):
super().__init__()
self.l1 = nn.Linear(400, 200)
self.l2 = nn.Linear(200, 100)
def forward(self, data):
h = relu(self.l1(data))
a = self.l2(h)
return a[:, 0:50], softplus(a[:, 50:])
encode = Encoder()
# Takes the guide RNN hidden state to parameters of
# the guide distributions over z_where and z_pres.
class Predict(nn.Module):
def __init__(self, ):
super().__init__()
self.l = nn.Linear(256, 7)
def forward(self, h):
a = self.l(h)
z_pres_p = sigmoid(a[:, 0:1]) # Squish to [0,1]
z_where_loc = a[:, 1:4]
z_where_scale = softplus(a[:, 4:]) # Squish to >0
return z_pres_p, z_where_loc, z_where_scale
predict = Predict()
def guide_step_improved(t, data, prev):
rnn_input = torch.cat((data, prev.z_where, prev.z_what, prev.z_pres), 1)
h, c = rnn(rnn_input, (prev.h, prev.c))
z_pres_p, z_where_loc, z_where_scale = predict(h)
z_pres = pyro.sample('z_pres_{}'.format(t),
dist.Bernoulli(z_pres_p * prev.z_pres)
.to_event(1))
z_where = pyro.sample('z_where_{}'.format(t),
dist.Normal(z_where_loc, z_where_scale)
.to_event(1))
# New. Crop a small window from the input.
x_att = image_to_object(z_where, data)
# Compute the parameter of the distribution over z_what
# by passing the window through the encoder network.
z_what_loc, z_what_scale = encode(x_att)
z_what = pyro.sample('z_what_{}'.format(t),
dist.Normal(z_what_loc, z_what_scale)
.to_event(1))
return # values for next step
以下是实现此改进引导网络的方法,以及所涉及网络的详细实现
[15]:
def z_where_inv(z_where):
# Take a batch of z_where vectors, and compute their "inverse".
# That is, for each row compute:
# [s,x,y] -> [1/s,-x/s,-y/s]
# These are the parameters required to perform the inverse of the
# spatial transform performed in the generative model.
n = z_where.size(0)
out = torch.cat((torch.ones([1, 1]).type_as(z_where).expand(n, 1), -z_where[:, 1:]), 1)
out = out / z_where[:, 0:1]
return out
def image_to_object(z_where, image):
n = image.size(0)
theta_inv = expand_z_where(z_where_inv(z_where))
grid = affine_grid(theta_inv, torch.Size((n, 1, 20, 20)))
out = grid_sample(image.view(n, 1, 50, 50), grid)
return out.view(n, -1)
由于我们希望保持引导网络的可微性,我们再次使用 STN 来执行所需的“裁剪”。image_to_object 函数执行与引导网络中使用的 object_to_image 函数相反的变换。也就是说,前者将小图像放置到大图像上,而后者从大图像中裁剪出小图像。
另一个视角¶
到目前为止,我们孤立地考虑了模型和引导网络,但如果我们拉远镜头,从整体上看待模型和引导网络的计算,就会获得一个有趣的视角。这样做,我们看到在每个步骤中,AIR 都包含一个子计算,其结构与变分自编码器 (VAE) 的结构相同。
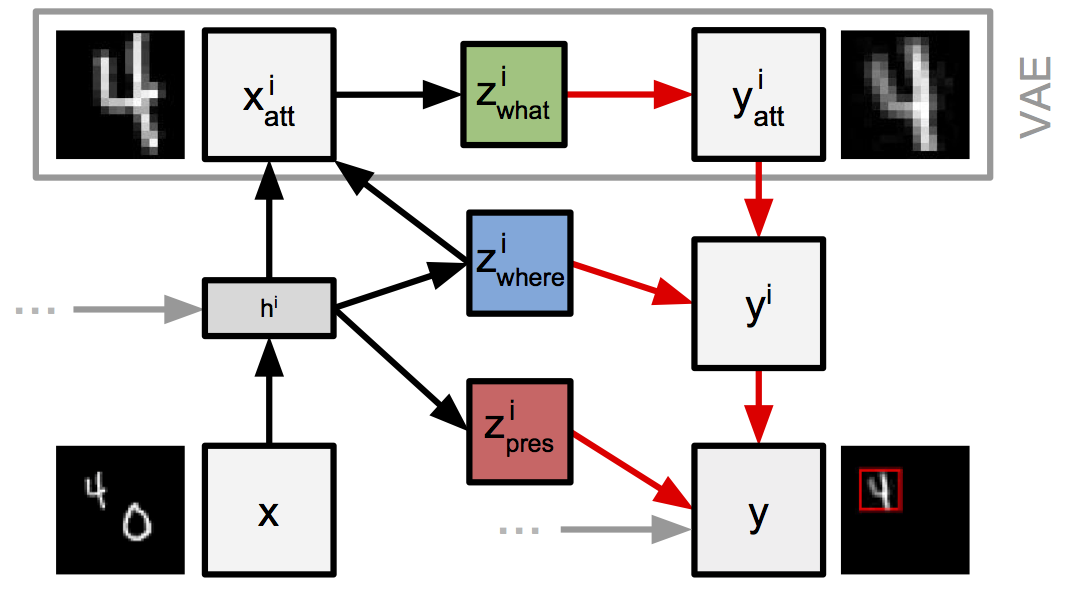
图 2:引导网络与模型在每个步骤中的交互。
从这个角度来看,AIR 被视为 VAE 的序列变体。从输入图像中裁剪小窗口的行为旨在将 VAE 的注意力在每个步骤中限制到输入图像的一小块区域;因此得名“Attend, Infer, Repeat”。
推断¶
正如我们在简介中提到的,在此模型中成功执行推断是一个挑战。特别是,模型中存在离散选择使得推断比所有选择都可以重参数化的模型更棘手。我们面临的根本问题是,变分推断中使用的梯度估计在存在不可重参数化选择时方差要高得多。
为了控制这种方差,论文将一种称为“数据依赖基线”(又称“神经基线”)的技术应用于模型中的离散选择。
数据依赖基线¶
对我们来说幸运的是,Pyro 支持数据依赖基线。如果您对此概念还不熟悉,可能需要在继续阅读之前阅读我们的介绍。作为模型作者,我们只需要实现神经网络,将数据作为输入传递给它,并将其输出馈送给 pyro.sample。Pyro 的推断后端将确保基线包含在用于推断的梯度估计器中,并且网络参数得到适当更新。
让我们看看如何将数据依赖基线添加到我们的 AIR 实现中。我们需要一个神经网络,它能够在引导网络中的每个离散选择处输出一个(标量)基线值,其输入包括 multi-mnist 图像以及引导网络迄今为止采样到的值。请注意,这与引导网络的结构非常相似,事实上我们也将再次使用一个循环网络。
[16]:
bl_rnn = nn.LSTMCell(2554, 256)
bl_predict = nn.Linear(256, 1)
# Use an RNN to compute the baseline value. This network takes the
# input images and the values samples so far as input.
def baseline_step(x, prev):
rnn_input = torch.cat((x,
prev.z_where.detach(),
prev.z_what.detach(),
prev.z_pres.detach()), 1)
bl_h, bl_c = bl_rnn(rnn_input, (prev.bl_h, prev.bl_c))
bl_value = bl_predict(bl_h) * prev.z_pres
return bl_value, bl_h, bl_c
为了实现这一点,我们首先编写一个简短的辅助函数,它实现我们刚刚描述的 RNN 的一个步骤
这里有两个重要的细节需要强调
首先,我们在将引导网络采样的值传递给基线网络之前,对这些值进行 detach 操作。这很重要,因为基线网络和引导网络是完全独立的网络,使用不同的目标进行优化。如果不这样做,梯度将从基线网络流向引导网络。在使用数据依赖基线时,每当我们把引导网络采样的值馈送给基线网络时,都必须进行此操作。(如果我们不这样做,将触发 PyTorch 运行时错误。)
其次,我们将基线网络的输出乘以来自前一步的 z_pres 值。这减轻了基线网络为已完成样本输出准确预测的负担。(已完成样本的输出将乘以零,因此这些输出的基线损失的导数将为零。)这样做是没问题的,因为实际上我们已经从推断目标中移除了已完成样本的随机选择,因此无需对它们应用任何方差缩减。
我们现在拥有了完成引导网络实现所需的一切。
guide_step函数将与上面介绍的guide_step_improved非常相似。唯一的改变是我们现在调用
baseline_step辅助函数,并将其返回的基线值传递给pyro.sample。
我们现在对已完成样本的 z_where 和 z_what 选择进行掩码。这与添加到模型的掩码的作用完全相同。(请参阅前面的讨论了解此更改背后的动机。)
[17]:
GuideState = namedtuple('GuideState', ['h', 'c', 'bl_h', 'bl_c', 'z_pres', 'z_where', 'z_what'])
def initial_guide_state(n):
return GuideState(h=torch.zeros(n, 256),
c=torch.zeros(n, 256),
bl_h=torch.zeros(n, 256),
bl_c=torch.zeros(n, 256),
z_pres=torch.ones(n, 1),
z_where=torch.zeros(n, 3),
z_what=torch.zeros(n, 50))
def guide_step(t, data, prev):
rnn_input = torch.cat((data, prev.z_where, prev.z_what, prev.z_pres), 1)
h, c = rnn(rnn_input, (prev.h, prev.c))
z_pres_p, z_where_loc, z_where_scale = predict(h)
# Here we compute the baseline value, and pass it to sample.
baseline_value, bl_h, bl_c = baseline_step(data, prev)
z_pres = pyro.sample('z_pres_{}'.format(t),
dist.Bernoulli(z_pres_p * prev.z_pres)
.to_event(1),
infer=dict(baseline=dict(baseline_value=baseline_value.squeeze(-1))))
z_where = pyro.sample('z_where_{}'.format(t),
dist.Normal(z_where_loc, z_where_scale)
.mask(z_pres)
.to_event(1))
x_att = image_to_object(z_where, data)
z_what_loc, z_what_scale = encode(x_att)
z_what = pyro.sample('z_what_{}'.format(t),
dist.Normal(z_what_loc, z_what_scale)
.mask(z_pres)
.to_event(1))
return GuideState(h=h, c=c, bl_h=bl_h, bl_c=bl_c, z_pres=z_pres, z_where=z_where, z_what=z_what)
def guide(data):
# Register networks for optimization.
pyro.module('rnn', rnn),
pyro.module('predict', predict),
pyro.module('encode', encode),
pyro.module('bl_rnn', bl_rnn)
pyro.module('bl_predict', bl_predict)
with pyro.plate('data', data.size(0), subsample_size=64) as indices:
batch = data[indices]
state = initial_guide_state(batch.size(0))
steps = []
for t in range(3):
state = guide_step(t, batch, state)
steps.append(state)
return steps
我们还将编写一个 guide 函数,它将迭代调用 guide_step,为整个模型提供一个引导网络。
整合所有部分¶
[18]:
data = mnist.view(-1, 50 * 50)
svi = SVI(model,
guide,
optim.Adam({'lr': 1e-4}),
loss=TraceGraph_ELBO())
for i in range(5):
loss = svi.step(data)
print('i={}, elbo={:.2f}'.format(i, loss / data.size(0)))
i=0, elbo=2806.79
i=1, elbo=3656.81
i=2, elbo=3222.37
i=3, elbo=3872.77
i=4, elbo=2818.27
我们现在已经完成了模型和引导网络的实现。正如我们在之前的教程中看到的,我们只需再编写几行代码就可以开始执行推断了
这里一个关键的细节是,我们使用了 TraceGraph_ELBO 损失而不是更简单的 Trace_ELBO。这表明我们希望使用支持数据依赖基线的梯度估计器。该估计器还通过利用模型中包含的独立性信息来减少梯度估计的方差。类似的方法在 [1] 中隐式使用,并且是在此模型上获得良好结果所必需的。
结果¶
为了验证我们的实现,我们使用了独立实现运行了推断,并将其性能与 [1] 中报告的一些结果进行了比较。
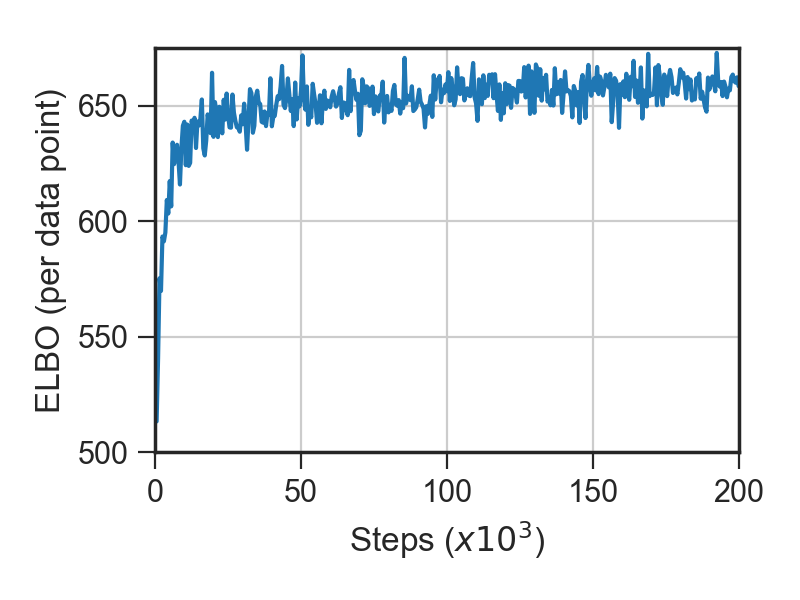

图 3:左图:优化过程中证据下界 (ELBO) 的进展。右图:优化过程中训练集计数准确率的进展。
计数准确率达到约 98.7%,这与 [1] 中报告的计数准确率大致相同。ELBO 达到的值与 [1] 中报告的值略有不同,这可能是由于使用的先验存在微小差异。

z_pres 和 z_where 的采样值。参照 [1],第一、第二和第三步分别使用红色、绿色和蓝色边框显示。(由于引导网络对这些样本都没有使用三步,所以没有显示蓝色边框。)它还显示了将从引导网络中采样的隐变量重新通过模型生成输出图像而获得的输入重建。图 4:顶行:multi-mnist 测试集中的数据点。底行:引导网络样本的可视化以及模型对输入的重建。
python main.py -n 200000 -blr 0.1 --z-pres-prior 0.01 --scale-prior-sd 0.2 --predict-net 200 --bl-predict-net 200 --decoder-output-use-sigmoid --decoder-output-bias -2 --seed 287710
这些结果使用以下参数收集
我们使用了 Pyro commit c0b38ad 和 PyTorch 0.2.0.post4。推断在 NVIDIA K80 GPU 上运行了大约 4 小时。(注意,即使我们设置了随机种子,在使用 CUDA 时,这也不足以使推断具有确定性。)
实践中¶
我们发现在使用 AIR 获得良好结果时,注意以下细节非常重要。
除非对
z_pres使用较小的先验成功概率,否则推断不太可能恢复正确的对象计数。在 [1] 中,这种概率在优化过程中从接近 1 的值退火到1e-5(或更小),尽管我们发现固定值约为0.01在我们的实现中效果很好。我们最初将解码器网络初始化为主要生成空对象。(使用
--decoder-output-bias参数。)这鼓励引导网络在优化早期探索使用对象来解释输入。如果没有这样做,每个对象都是一个中灰色方块,这会被似然函数严厉惩罚,促使引导网络关闭大部分步骤。
据报道,在实践中使用不同的学习率进行基线网络优化是有益的。这在 Pyro 中很容易实现,只需标记与基线网络相关的模块,并将多个学习率传递给优化器即可。(有关更多详细信息,请参阅 SVI 教程第一部分的优化器部分。)在 [1] 中,引导网络使用了 1e-4 的学习率,基线网络使用了 1e-3 的学习率。我们发现有必要为基线网络使用更大的学习率,以便以与 [1] 相似的速度在计数准确率上取得进展。这种差异可能是由于 Pyro 设置了略有不同的基线损失导致的。
参考文献¶
[2] 空间变换网络 Max Jaderberg and Karen Simonyan and Andrew Zisserman