半监督 VAE

引言

我们在教程中介绍的大多数模型都是无监督的

我们还介绍了一个简单的有监督模型

半监督设置代表了一个有趣的中间情况，其中一部分数据已标记，一部分未标记。这在实践中也具有重要意义，因为我们通常只有很少的标记数据而有大量的未标记数据。我们显然希望利用标记数据来改进我们对未标记数据的模型。

半监督设置也非常适合生成模型，生成模型可以很自然地处理缺失数据——至少在概念上如此。正如我们将看到的，在我们将注意力限制在半监督生成模型时，会有各种不同的模型变体和可能的推断策略。尽管我们只能详细探索其中一些变体，但希望本教程能让您对概率编程提供的抽象和模块化有更深的认识。

因此，让我们构建一个生成模型。我们有一个数据集 \(\mathcal{D}\) 包含 \(N\) 个数据点，

\[\mathcal{D} = \{ ({\bf x}_i, {\bf y}_i) \}\]

其中 \(\{ {\bf x}_i \}\) 总是被观察到的，而标签 \(\{ {\bf y}_i \}\) 只在数据的某个子集中被观察到。由于我们希望能够对数据的复杂变化进行建模，我们将构建一个包含局部隐变量 \({\bf z}_i\) 的隐变量模型，其中每个 \(({\bf x}_i, {\bf y}_i)\) 对都有其私有的 \({\bf z}_i\)。即使选择了这些设定，仍有多种模型变体可能：我们将重点关注图 1 所示的模型变体（这是参考文献 [1] 中的模型 M2）。

图 1：我们的半监督生成模型（参见参考文献 [1] 中的模型 M2）

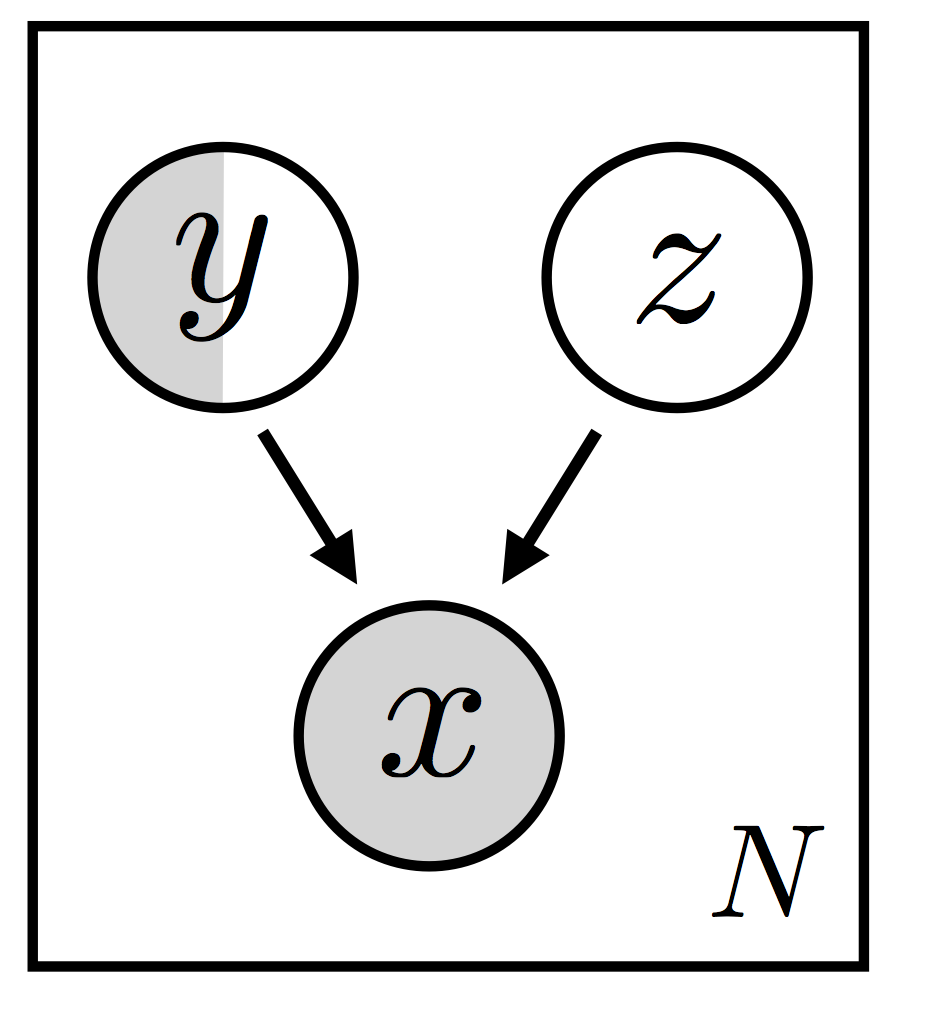
为方便起见——也因为我们将在下面的实验中对 MNIST 进行建模——假设 \(\{ {\bf x}_i \}\) 是图像，而 \(\{ {\bf y}_i \}\) 是数字标签。在这种模型设置中，隐随机变量 \({\bf z}_i\) 和（部分观察到的）数字标签 共同 生成观察到的图像。\({\bf z}_i\) 代表了 除 数字标签以外的所有信息，可能是手写风格或位置。我们暂且不讨论何时这种特定的 \(({\bf x}_i, {\bf y}_i, {\bf z}_i)\) 分解是合适的，因为这个问题的答案很大程度上取决于所使用的数据集（以及其他因素）。相反，我们将强调在此模型中进行推断所面临的一些挑战以及我们将在本教程其余部分探索的一些解决方案。

推断的挑战

为具体起见，我们将继续假设部分观察到的 \(\{ {\bf y}_i \}\) 是离散标签；我们还将假设 \(\{ {\bf z}_i \}\) 是连续的。

  • 如果我们将随机变分推断的一般方法应用于我们的模型（参见SVI 第一部分），则每当离散（因此不可重参数化）变量 \({\bf y}_i\) 未观察到时，我们将对其进行采样。正如SVI 第三部分中所讨论的，这通常会导致高方差的梯度估计。

  • 一种缓解此问题的常用方法——也是我们将在下面探讨的方法——是放弃采样，转而在计算未标记数据点 \({\bf x}_i\) 的 ELBO 时，对类别标签 \({\bf y}_i\) 的所有十个值进行求和。这会增加每一步的计算成本，但可以帮助我们降低梯度估计器的方差，从而减少所需的步骤数。

  • 回想一下，guide 的作用是“填补”隐 随机变量。具体来说，我们的 guide 的一个组成部分将是一个数字分类器 \(q_\phi({\bf y} | {\bf x})\)，它将根据图像 \(\{ {\bf x}_i \}\) 随机“填补”标签 \(\{ {\bf y}_i \}\)。关键是，这意味着 ELBO 中唯一依赖于 \(q_\phi(\cdot | {\bf x})\) 的项是涉及对 未标记 数据点求和的项。这意味着我们的分类器 \(q_\phi(\cdot | {\bf x})\)——这在许多情况下是主要的关注对象——将不会从标记的数据点中学习（至少不是直接学习）。

  • 这似乎是一个潜在的问题。幸运的是，有多种可能的修复方法。下面我们将遵循参考文献 [1] 中的方法，该方法引入了一个额外的分类器目标函数，以确保分类器直接从标记数据中学习。

我们任务艰巨，所以让我们开始吧！

第一个变体：标准目标函数，朴素估计器

正如引言中所讨论的，我们正在考虑图 1 中所示的模型。更详细地说，模型的结构如下：

  • \(p({\bf y}) = Cat({\bf y}~|~{\bf \pi})\): 类别标签的多项式（或分类）先验

  • \(p({\bf z}) = \mathcal{N}({\bf z}~|~{\bf 0,I})\): 隐编码 \(\bf z\) 的单位正态先验

  • \(p_{\theta}({\bf x}~|~{\bf z,y}) = Bernoulli\left({\bf x}~|~\mu\left({\bf z,y}\right)\right)\): 参数化的 Bernoulli 似然函数；\(\mu\left({\bf z,y}\right)\) 对应于代码中的 decoder

我们构建 guide \(q_{\phi}(.)\) 的组成部分如下：

  • \(q_{\phi}({\bf y}~|~{\bf x}) = Cat({\bf y}~|~{\bf \alpha}_{\phi}\left({\bf x}\right))\): 参数化的多项式（或分类）分布；\({\bf \alpha}_{\phi}\left({\bf x}\right)\) 对应于代码中的 encoder_y

  • \(q_{\phi}({\bf z}~|~{\bf x, y}) = \mathcal{N}({\bf z}~|~{\bf \mu}_{\phi}\left({\bf x, y}\right), {\bf \sigma^2_{\phi}\left(x, y\right)})\): 参数化的正态分布；\({\bf \mu}_{\phi}\left({\bf x, y}\right)\) 和 \({\bf \sigma^2_{\phi}\left(x, y\right)}\) 对应于代码中的神经数字分类器 encoder_z

这些选择再现了参考文献 [1] 中模型 M2 及其对应推断网络的结构。

我们在下面将此模型和 guide 对转换为 Pyro 代码。请注意：

  • 标签 ys（使用独热编码表示）仅部分观察到（None 表示未观察到的值）。

  • model() 处理观察到和未观察到的情况。

  • 代码假设 xs 和 ys 分别是图像和标签的小批量数据，每个批次的大小由 batch_size 表示。

[ ]:

def model(self, xs, ys=None):
    # register this pytorch module and all of its sub-modules with pyro
    pyro.module("ss_vae", self)
    batch_size = xs.size(0)

    # inform Pyro that the variables in the batch of xs, ys are conditionally independent
    with pyro.plate("data"):

        # sample the handwriting style from the constant prior distribution
        prior_loc = xs.new_zeros([batch_size, self.z_dim])
        prior_scale = xs.new_ones([batch_size, self.z_dim])
        zs = pyro.sample("z", dist.Normal(prior_loc, prior_scale).to_event(1))

        # if the label y (which digit to write) is supervised, sample from the
        # constant prior, otherwise, observe the value (i.e. score it against the constant prior)
        alpha_prior = xs.new_ones([batch_size, self.output_size]) / (1.0 * self.output_size)
        ys = pyro.sample("y", dist.OneHotCategorical(alpha_prior), obs=ys)

        # finally, score the image (x) using the handwriting style (z) and
        # the class label y (which digit to write) against the
        # parametrized distribution p(x|y,z) = bernoulli(decoder(y,z))
        # where `decoder` is a neural network
        loc = self.decoder([zs, ys])
        pyro.sample("x", dist.Bernoulli(loc).to_event(1), obs=xs)

def guide(self, xs, ys=None):
    with pyro.plate("data"):
        # if the class label (the digit) is not supervised, sample
        # (and score) the digit with the variational distribution
        # q(y|x) = categorical(alpha(x))
        if ys is None:
            alpha = self.encoder_y(xs)
            ys = pyro.sample("y", dist.OneHotCategorical(alpha))

        # sample (and score) the latent handwriting-style with the variational
        # distribution q(z|x,y) = normal(loc(x,y),scale(x,y))
        loc, scale = self.encoder_z([xs, ys])
        pyro.sample("z", dist.Normal(loc, scale).to_event(1))

网络定义

在我们的实验中，我们使用与参考文献 [1] 相同的网络配置。编码器和解码器网络有一个隐藏层，包含 \(500\) 个隐藏单元和 softplus 激活函数。我们使用 softmax 作为 encoder_y 输出的激活函数，使用 sigmoid 作为 decoder 输出的激活函数，并对 encoder_z 输出的尺度部分进行指数化。隐变量维度为 50。

MNIST 预处理

我们将像素值归一化到范围 \([0.0, 1.0]\)。我们使用 torchvision 库中的 MNIST 数据加载器。测试集包含 \(10000\) 个样本。默认训练集包含 \(60000\) 个样本。我们使用前 \(50000\) 个样本进行训练（分为有监督和无监督部分），剩余的 \(10000\) 张图像用于验证。对于我们的实验，我们在训练集使用了 \(4\) 种监督配置，即我们考虑随机选择 \(3000\)、\(1000\)、\(600\) 和 \(100\) 个有监督样本（同时确保每个类别均衡）。

目标函数

此模型的目标函数包含两个项（参见参考文献 [1] 中的公式 8）

\[\mathcal{J} = \!\!\sum_{({\bf x,y}) \in \mathcal{D}_{supervised} } \!\!\!\!\!\!\!\!\mathcal{L}\big({\bf x,y}\big) +\!\!\! \sum_{{\bf x} \in \mathcal{D}_{unsupervised}} \!\!\!\!\!\!\!\mathcal{U}\left({\bf x}\right)\]

为了在 Pyro 中实现这一点，我们设置了一个 SVI 类的单一实例。目标函数中的两个不同项将根据我们传递给 step 方法的是标记数据还是未标记数据而自动出现。我们将轮流使用标记和未标记的小批量数据进行步骤，每种类型小批量数据的步骤数取决于数据的标记总比例。例如，如果我们有 1,000 张标记图像和 49,000 张未标记图像，那么对于每个标记小批量，我们将使用未标记小批量进行 49 个步骤。（请注意，有不同的方法可以实现这一点，但为简单起见，我们仅考虑此变体。）此设置的代码如下所示：

[ ]:

from pyro.infer import SVI, Trace_ELBO, TraceEnum_ELBO, config_enumerate
from pyro.optim import Adam

# setup the optimizer
adam_params = {"lr": 0.0003}
optimizer = Adam(adam_params)

# setup the inference algorithm
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())

当我们在 Pyro 中运行此推断时，测试时看到的性能会因分类变量采样固有的噪声而降低（参见本教程末尾的图 2 和表 1）。为了解决这个问题，我们将需要一个更好的 ELBO 梯度估计器。

图 2：变体 1 （左）3000 个有监督样本情况下的训练损失。（右）测试和验证准确率。

插曲：对离散隐变量求和

正如引言中所强调的，当离散隐标签 \({\bf y}\) 未观察到时，ELBO 梯度估计依赖于从 \(q_\phi({\bf y}|{\bf x})\) 中采样。这些梯度估计可能方差很高，尤其是在学习过程的早期，此时猜测的标签通常不正确。在这种情况下降低方差的常用方法是对离散隐变量进行求和，用显式求和代替蒙特卡罗期望，即

\[\mathbb E_{{\bf y}\sim q_\phi(\cdot|{\bf x})}\nabla\operatorname{ELBO}\]

用显式求和

\[\sum_{\bf y} q_\phi({\bf y}|{\bf x})\nabla\operatorname{ELBO}\]

这种求和通常像 [1] 中那样手动实现，但在许多情况下 Pyro 可以自动完成。要自动对所有离散隐变量（此处仅为 \({\bf y}\)）求和，我们只需将 guide 包装在 config_enumerate() 中：

svi = SVI(model, config_enumerate(guide), optimizer, loss=TraceEnum_ELBO(max_plate_nesting=1))

在这种操作模式下，每个 svi.step(...) 会计算 \(y\) 的十个隐状态中的每一个的梯度项。尽管这样每一步会贵 \(10\times\)，但我们会看到较低方差的梯度估计抵消了额外的成本。

除了本教程中的特定模型，Pyro 支持对任意数量的离散隐变量求和。请注意，求和的成本是离散变量数量的指数级，但如果将多个独立的离散变量打包到单个张量中（如本教程中，整个小批次的离散标签打包到单个张量 \({\bf y}\) 中），则成本会较低（或更低）。要使用这种并行形式的 config_enumerate()，我们必须通过将矢量化代码包装在 with pyro.plate("name") 块中来告知 Pyro 小批次中的项目确实是独立的。

第二个变体：标准目标函数，更好的估计器

现在我们有了对离散隐变量求和的工具，我们可以看看这样做是否能提升性能。首先，从图 3 中可以看出，测试和验证准确率在训练过程中演变得更加平滑。更重要的是，仅此一项修改就将 \(3000\) 个标记样本情况下的测试准确率从 20% 左右提高到约 90%。完整结果请参见表 1。这很棒，但我们能做得更好吗？

图 3：变体 2 （左）3000 个有监督样本情况下的训练损失。（右）测试和验证准确率。

第三个变体：向目标函数添加项

对于我们目前探索的两个变体，分类器 \(q_{\phi}({\bf y}~|~ {\bf x})\) 没有直接从标记数据中学习。正如我们在引言中讨论的，这似乎是一个潜在的问题。解决此问题的一种方法是向目标函数添加一个额外项，以便分类器直接从标记数据中学习。请注意，这正是参考文献 [1] 中采用的方法（参见其公式 9）。修改后的目标函数如下所示：

\begin{align} \mathcal{J}^{\alpha} &= \mathcal{J} + \alpha \mathop{\mathbb{E}}_{\tilde{p_l}({\bf x,y})} \big[-\log\big(q_{\phi}({\bf y}~|~ {\bf x})\big)\big] \\ &= \mathcal{J} + \alpha' \sum_{({\bf x,y}) \in \mathcal{D}_{\text{supervised}}} \big[-\log\big(q_{\phi}({\bf y}~|~ {\bf x})\big)\big] \end{align}

其中 \(\tilde{p_l}({\bf x,y})\) 是标记（或有监督）数据上的经验分布，\(\alpha' \equiv \frac{\alpha}{|\mathcal{D}_{\text{supervised}}|}\)。请注意，我们引入了一个任意的超参数 \(\alpha\)，它调节新项的重要性。

为了在 Pyro 中使用此修改后的目标函数进行学习，我们执行以下操作：

  • 我们使用一个新的模型和 guide 对（参见下面的代码片段），它对应于针对给定图像 \({\bf x}\) 的预测分布 \(q_{\phi}({\bf y}~|~ {\bf x})\) 对观察到的标签 \({\bf y}\) 进行评分

  • 我们通过使用 poutine.scale 在 pyro.sample 调用中指定缩放因子 \(\alpha'\)（代码中的 aux_loss_multiplier）。请注意，poutine.scale 在 深度马尔可夫模型 中也用于类似目的，以实现 KL 退火。

  • 我们创建一个新的 SVI 对象，并使用它在新目标项上执行梯度步骤

[ ]:

def model_classify(self, xs, ys=None):
    pyro.module("ss_vae", self)
    with pyro.plate("data"):
        # this here is the extra term to yield an auxiliary loss
        # that we do gradient descent on
        if ys is not None:
            alpha = self.encoder_y(xs)
            with pyro.poutine.scale(scale=self.aux_loss_multiplier):
                pyro.sample("y_aux", dist.OneHotCategorical(alpha), obs=ys)

def guide_classify(xs, ys):
    # the guide is trivial, since there are no
    # latent random variables
    pass

svi_aux = SVI(model_classify, guide_classify, optimizer, loss=Trace_ELBO())

当我们在 Pyro 中运行带有附加目标项的推断时，我们优于之前的两种推断设置。例如，对于 \(3000\) 个标记样本的情况，测试准确率从 90% 提高到 96%（参见下面的图 4 和下一节中的表 1）。请注意，我们使用验证准确率来选择超参数 \(\alpha'\)。

图 4：变体 3 （左）3000 个有监督样本情况下的训练损失。（右）测试和验证准确率。

结果

有监督数据

第一个变体

第二个变体

第三个变体

基准分类器

100

0.2007(0.0353)

0.2254(0.0346)

0.9319(0.0060)

0.7712(0.0159)

600

0.1791(0.0244)

0.6939(0.0345)

0.9437(0.0070)

0.8716(0.0064)

1000

0.2006(0.0295)

0.7562(0.0235)

0.9487(0.0038)

0.8863(0.0025)

3000

0.1982(0.0522)

0.8932(0.0159)

0.9582(0.0012)

0.9108(0.0015)

表 1：不同推断方法的结果准确率（含 95% 置信区间）

表 1 汇总了本教程中探索的三个变体的结果。作为比较，我们还展示了一个简单分类器基准的结果，该基准仅使用有监督数据（不使用隐随机变量）。报告的是对五次随机选择的有监督数据计算的平均准确率（括号中为 95% 置信区间）。

我们首先注意到，第三个变体（我们对离散隐随机变量 \(\bf y\) 求和并使用了目标函数中的额外项）的结果与参考文献 [1] 中报告的结果一致。这是令人鼓舞的，因为它意味着 Pyro 中的抽象足够灵活，可以适应所需的建模和推断设置。重要的是，这种灵活性显然是超越基准所必需的。同样值得强调的是，随着标记数据点数量的减少，我们的生成模型设置的基准与第三个变体之间的差距会增加（在只有 100 个标记数据点的情况下达到约 15% 的最大差距）。这是一个诱人的结果，因为正是在标记数据点较少的情况下，半监督学习才显得尤为吸引人。

隐空间可视化

图 5：变体 3 在 3000 个有监督样本情况下的隐空间嵌入

我们使用 T-SNE 将隐变量 \(\bf z\) 的维度从 \(50\) 降到 \(2\)，并在图 5 中可视化了 10 个数字类别。请注意，嵌入的结构与 VAE 情况下的结构有很大不同，在 VAE 中，数字在嵌入空间中是清晰分离的。这很合理，因为在半监督情况下，隐变量 \(\bf z\) 可以自由地利用其表示能力来建模例如手写风格等，因为数字之间的变化由（部分观察到的）标签提供。

条件图像生成

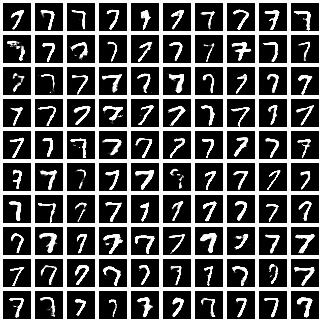
图 6：通过固定类别标签并改变 z 获得的条件样本（针对 3000 个有监督样本情况下的变体 3）

我们通过对隐变量 \({\bf z}\) 采样不同的值，为每个类别标签（从 \(0\) 到 \(9\)）采样了 \(100\) 张图像。每个数字展示的手写风格多样性与我们在 T-SNE 可视化中看到的一致，表明 \(\bf z\) 学习到的表示与类别标签是解耦的。

总结

我们已经看到，生成模型为半监督机器学习提供了一种自然的方法。生成模型最吸引人的特点之一是，我们可以在一个统一的环境中探索各种各样的模型。在本教程中，我们只能探索可能模型和推断设置的一小部分。没有理由期望某一个变体是最好的；根据数据集和应用的不同，会倾向于选择某一种变体。而且，还有很多变体（参见图 7）！

图 7：半监督生成模型的动物园

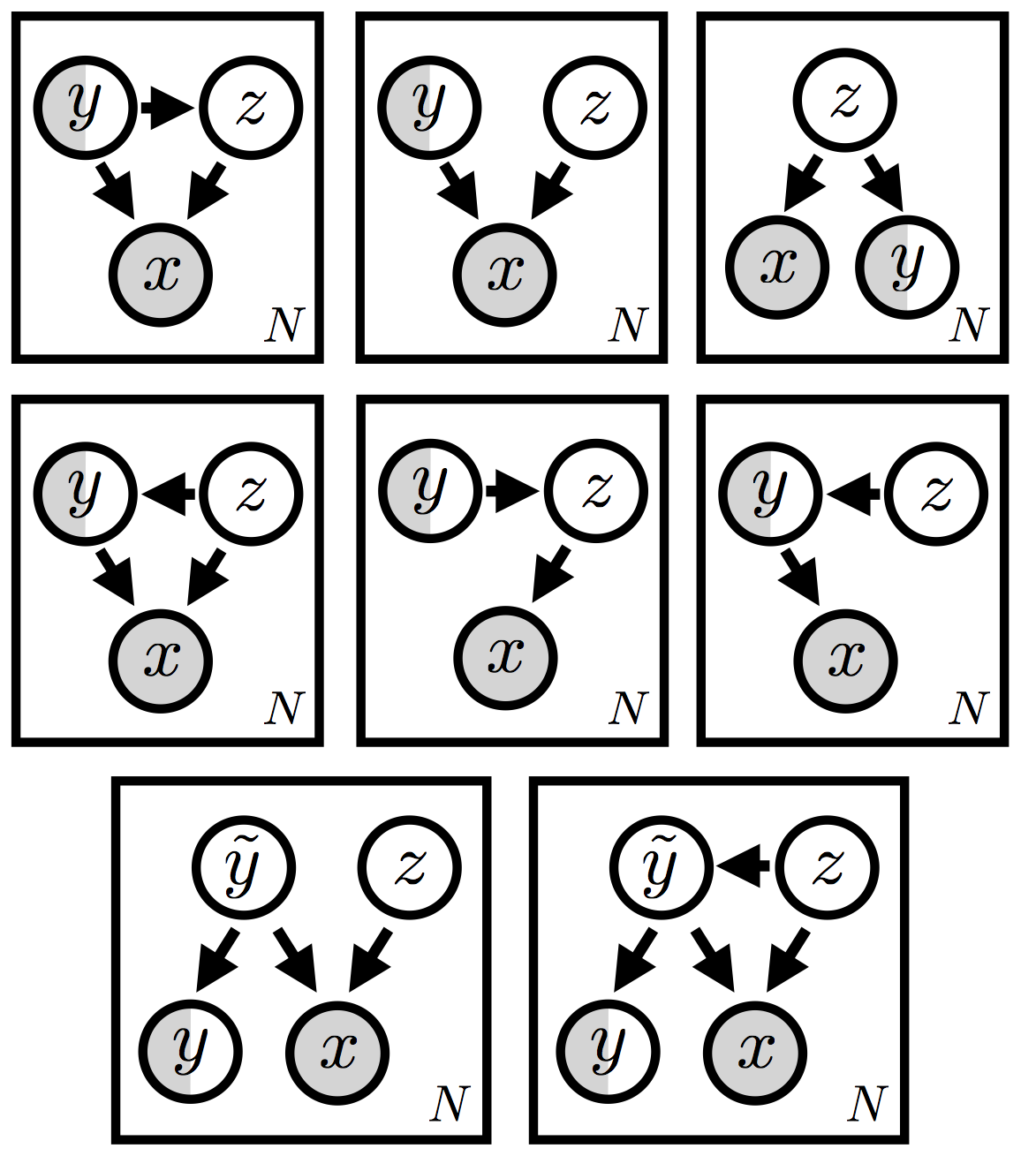
其中一些变体显然比其他变体更有意义，但先验地很难知道哪些值得尝试。一旦我们涉足更复杂的设置，比如图底部包含一个除了部分观察到的标签 \({\bf y}\) 之外始终存在的隐随机变量 \(\tilde{\bf y}\) 的两个模型，尤其如此。（顺便说一句，这类模型——参见参考文献 [2] 中类似变体——提供了解决我们上面提到的“无训练”问题的另一种潜在方案。）

读者可能不需要被说服就知道，如果每个模型和每个推断过程都从头编写代码，系统地探索哪怕是这些选项的一小部分也将极其耗时且容易出错。只有通过概率编程系统实现的模块化和抽象，我们才能有望以任何形式的灵活性探索生成模型的全貌——并收获随之而来的成果。

在 Github 上查看完整代码。

参考文献

Semi-supervised Learning with Deep Generative Models,     Diederik P. Kingma, Danilo J. Rezende, Shakir Mohamed, Max Welling

Learning Disentangled Representations with Semi-Supervised Deep Generative Models,      N. Siddharth, Brooks Paige, Jan-Willem Van de Meent, Alban Desmaison, Frank Wood,      Noah D. Goodman, Pushmeet Kohli, Philip H.S. Torr