使用归一化流引导的SVI

归功于它们的表达能力，归一化流（参见 归一化流简介）是随机变分推断 (SVI) 的优秀引导候选。本notebook演示了如何使用归一化流作为引导执行摊销SVI。

在本notebook中，我们使用 Zuko 实现归一化流，但使用其他基于PyTorch的流库也能获得类似结果。

import pyro
import torch
import zuko  # pip install zuko

from corner import corner, overplot_points  # pip install corner
from pyro.contrib.zuko import ZukoToPyro
from pyro.optim import ClippedAdam
from pyro.infer import SVI, Trace_ELBO
from torch import Tensor

模型

我们定义了一个简单的非线性模型 \(p(x | z)\)，其隐变量 \(z\) 上有一个标准高斯先验 \(p(z)\)。

prior = pyro.distributions.Normal(torch.zeros(3), torch.ones(3)).to_event(1)

def likelihood(z: Tensor):
    mu = z[..., :2]
    rho = z[..., 2].tanh() * 0.99

    cov = 1e-2 * torch.stack([
        torch.ones_like(rho), rho,
        rho, torch.ones_like(rho),
    ], dim=-1).unflatten(-1, (2, 2))

    return pyro.distributions.MultivariateNormal(mu, cov)

def model(x: Tensor):
    with pyro.plate("data", x.shape[1]):
        z = pyro.sample("z", prior)

        with pyro.plate("obs", 5):
            pyro.sample("x", likelihood(z), obs=x)

我们采样了64个参考隐变量和观测值 \((z^*, x^*)\)。实际上，\(z^*\) 是未知的，而 \(x^*\) 是你的数据。

z_star = prior.sample((64,))
x_star = likelihood(z_star).sample((5,))

引导

我们使用归一化流定义引导 \(q_\phi(z | x)\)。我们选择了一种条件 神经样条流，该流借鉴自 Zuko 库。由于Zuko分布与Pyro分布非常相似，因此一个简单的包装器 (ZukoToPyro) 足以使Zuko和Pyro完全兼容。

flow = zuko.flows.NSF(features=3, context=10, transforms=1, hidden_features=(256, 256))
flow.transform = flow.transform.inv  # inverse autoregressive flow (IAF) are fast to sample from

def guide(x: Tensor):
    pyro.module("flow", flow)

    with pyro.plate("data", x.shape[1]):  # amortized
        pyro.sample("z", ZukoToPyro(flow(x.transpose(0, 1).flatten(-2))))

SVI

我们使用标准的随机变分推断 (SVI) 流程来训练我们的引导。我们使用16个粒子来减少ELBO的方差，并裁剪梯度范数以使训练更稳定。

pyro.clear_param_store()

svi = SVI(model, guide, optim=ClippedAdam({"lr": 1e-3, "clip_norm": 10.0}), loss=Trace_ELBO(num_particles=16, vectorize_particles=True))

for step in range(4096 + 1):
    elbo = svi.step(x_star)

    if step % 256 == 0:
        print(f'({step})', elbo)

(0) 209195.08367919922
(256) -25.225540161132812
(512) -99.09033203125
(768) -102.66302490234375
(1024) -138.8058319091797
(1280) -92.15625
(1536) -136.78167724609375
(1792) -87.76119995117188
(2048) -116.21714782714844
(2304) -162.0266571044922
(2560) -91.13175964355469
(2816) -164.86270141601562
(3072) -98.17607116699219
(3328) -102.58432006835938
(3584) -151.61912536621094
(3840) -77.94436645507812
(4096) -121.82719421386719

后验预测

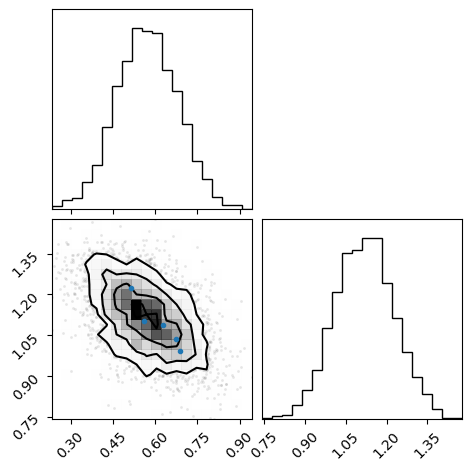
z = flow(x_star[:, 0].flatten()).sample((4096,))
x = likelihood(z).sample()

fig = corner(x.numpy())

overplot_points(fig, x_star[:, 0].numpy())

z = flow(x_star[:, 1].flatten()).sample((4096,))
x = likelihood(z).sample()

fig = corner(x.numpy())

overplot_points(fig, x_star[:, 1].numpy())