高维贝叶斯工作流程及其在 SARS-CoV-2 毒株中的应用¶

本教程描述了一种使用 Pyro 逐步构建分析高维数据流程的工作流程。该工作流程是我们在将 Pyro 应用于具有 \(10^5\) 个或更多潜变量的模型多年后演变而来的。我们在 Gelman 等人 (2020) 提出的贝叶斯工作流程概念的基础上，重点关注高维模型特有的方面：近似推断和数值稳定性。虽然流程中的各个组成部分值得单独进行教程讲解，但本教程侧重于如何逐步组合这些组成部分。

找到数据的好模型的最快方法是快速摒弃许多不好的模型，即进行迭代。在统计学中，我们将这种迭代工作流程称为 Box 循环。高效的工作流程使我们能够尽快摒弃坏模型。工作流程的效率要求对上游组件的代码更改不会破坏下游组件先前的编码工作。Pyro 应对这一挑战的方法包括变分近似的策略 (pyro.infer.autoguide) 以及转换模型坐标系以改善几何结构的策略 (pyro.infer.reparam)。

摘要¶

优秀模型只能通过迭代开发实现。
通过构建对代码更改具有鲁棒性的流程来快速迭代。
从简单模型和均场推断开始。
通过智能地初始化和使用 .clamp() 避免出现 NANs。
对模型重新参数化以改善几何结构。
通过结合使用 AutoGuides 或 EasyGuides 创建自定义变分族。

清洗数据
创建生成模型
使用均场推断进行初步检查
创建初始化启发式方法
对模型进行重新参数化
定制变分族：autoguides、easyguides、自定义 guides

概述¶

考虑从具有 \(10^5\) 个或更多连续潜变量的概率模型的后验分布中采样的问题，其数据可以完全载入内存。（对于更大的数据集，请考虑摊销变分推断。）即使已知后验是单峰或甚至对数凹的，由于潜变量之间的相关性，在此类高维模型中进行推断可能仍然具有挑战性。

为了在 Pyro 中对此类高维模型进行推断，我们发展了一种工作流程，以逐步构建结合变分推断、重新参数化效应和特殊初始化策略的数据分析流程。我们的工作流程总结为一系列步骤，其中任何步骤后的验证都可能建议回溯以更改前一步骤的设计决策。

清洗数据。
创建生成模型。
使用 MAP 或均场推断进行初步检查。
创建初始化启发式方法。
对模型重新参数化，并在均场 VI 下评估结果。
定制变分族 (autoguides, easyguides, custom guides)。

高效工作流程的关键在于确保更改不会破坏您的流程。也就是说，在构建了多个流程阶段、验证了结果并决定更改流程中的某个组件后，您希望最大限度地减少在其他组件中所需的代码更改。本教程的其余部分将单独描述这些步骤，然后描述各阶段之间交互的细微之处，最后提供一个示例。

运行示例：SARS-CoV-2 毒株预测¶

本教程中的运行示例是 Obermeyer 等人 (2022) 构建的 SARS-CoV-2 病毒不同毒株相对增长率模型，该模型基于公开数据，这些数据统计了全球在不同时间收集的病毒基因组样本中不同PANGO 谱系的数量。总共有大约 200 万个序列。

该模型是一个高维回归模型，包含大约 1000 个系数，使用简单的torch.softmax() 函数构建多元逻辑增长函数，并采用多项分布 (Multinomial) 的似然。尽管系数数量相对较少，但需要估计大约 50 万个局部潜变量，并且模型中的 plate 结构应该会产生近似分块对角线的后验协方差矩阵。关于使用同一数据集构建简单逻辑增长模型的介绍，请参阅逻辑增长教程。

[1]:

from collections import defaultdict
from pprint import pprint
import functools
import math
import os
import torch
import pyro
import pyro.distributions as dist
import pyro.poutine as poutine
from pyro.distributions import constraints
from pyro.infer import SVI, Trace_ELBO
from pyro.infer.autoguide import (
    AutoDelta,
    AutoNormal,
    AutoMultivariateNormal,
    AutoLowRankMultivariateNormal,
    AutoGuideList,
    init_to_feasible,
)
from pyro.infer.reparam import AutoReparam, LocScaleReparam
from pyro.nn.module import PyroParam
from pyro.optim import ClippedAdam
from pyro.ops.special import sparse_multinomial_likelihood
import matplotlib.pyplot as plt

if torch.cuda.is_available():
    print("Using GPU")
    torch.set_default_tensor_type("torch.cuda.FloatTensor")
else:
    print("Using CPU")
smoke_test = ('CI' in os.environ)

Using CPU

清洗数据¶

我们的运行示例将使用一个预先清洗好的数据集。我们首先使用 Nextstrain 的 ncov 工具进行预处理，然后使用 Broad Institute 的 pyro-cov 工具进行聚合，从而得到一个全球随时间变化的 SARS-CoV-2 谱系数据集。

[2]:

from pyro.contrib.examples.nextstrain import load_nextstrain_counts
dataset = load_nextstrain_counts()

def summarize(x, name=""):
    if isinstance(x, dict):
        for k, v in sorted(x.items()):
            summarize(v, name + "." + k if name else k)
    elif isinstance(x, torch.Tensor):
        print(f"{name}: {type(x).__name__} of shape {tuple(x.shape)} on {x.device}")
    elif isinstance(x, list):
        print(f"{name}: {type(x).__name__} of length {len(x)}")
    else:
        print(f"{name}: {type(x).__name__}")
summarize(dataset)

counts: Tensor of shape (27, 202, 1316) on cpu
features: Tensor of shape (1316, 2634) on cpu
lineages: list of length 1316
locations: list of length 202
mutations: list of length 2634
sparse_counts.index: Tensor of shape (3, 57129) on cpu
sparse_counts.total: Tensor of shape (27, 202) on cpu
sparse_counts.value: Tensor of shape (57129,) on cpu
start_date: datetime
time_step_days: int

创建生成模型¶

使用 Pyro 的第一步是创建一个生成模型，可以是 Python 函数，也可以是 pyro.nn.Module。从简单开始。从一个浅层层次结构开始，之后再添加潜变量以共享统计信息。从数据的一个切片开始，然后针对多个切片添加一个 plate。从简单分布开始，例如 Normal、LogNormal、Poisson 和 Multinomial，然后考虑过度分散的版本，例如 StudentT、Gamma、GammaPoisson/NegativeBinomial 和 DirichletMultinomial。保持模型简单易读，以便您可以共享它并从领域专家那里获得反馈。使用弱信息先验。

我们将重点介绍 Obermeyer 等人 (2022) 描述的竞争性 SARS-CoV-2 毒株的多元逻辑增长模型。该模型在其多项分布似然中使用了数值稳定的 logits 参数，而不是 probs 参数。类似地，上游变量 init、rate、rate_loc 和 coef 都处于对数空间。这意味着，例如，零系数的乘法效应为 1.0，正系数的乘法效应大于 1。

请注意，我们将 coef 按 1/100 缩放，因为我们想模拟一个非常小的数字，但 Pyro 和 PyTorch 的自动部分最适合数量级为 1.0 的数字，而不是非常小的数字。当我们稍后在火山图（volcano plot）中解释 coef 时，需要重复使用这个缩放因子。

[3]:

def model(dataset):
    features = dataset["features"]
    counts = dataset["counts"]
    assert features.shape[0] == counts.shape[-1]
    S, M = features.shape
    T, P, S = counts.shape
    time = torch.arange(float(T)) * dataset["time_step_days"] / 5.5
    time -= time.mean()
    strain_plate = pyro.plate("strain", S, dim=-1)
    place_plate = pyro.plate("place", P, dim=-2)
    time_plate = pyro.plate("time", T, dim=-3)

    # Model each region as multivariate logistic growth.
    rate_scale = pyro.sample("rate_scale", dist.LogNormal(-4, 2))
    init_scale = pyro.sample("init_scale", dist.LogNormal(0, 2))
    with pyro.plate("mutation", M, dim=-1):
        coef = pyro.sample("coef", dist.Laplace(0, 0.5))
    with strain_plate:
        rate_loc = pyro.deterministic("rate_loc", 0.01 * coef @ features.T)
    with place_plate, strain_plate:
        rate = pyro.sample("rate", dist.Normal(rate_loc, rate_scale))
        init = pyro.sample("init", dist.Normal(0, init_scale))
    logits = init + rate * time[:, None, None]

    # Observe sequences via a multinomial likelihood.
    with time_plate, place_plate:
        pyro.sample(
            "obs",
            dist.Multinomial(logits=logits.unsqueeze(-2), validate_args=False),
            obs=counts.unsqueeze(-2),
        )

该模型的执行成本主要由大型稀疏计数矩阵上的多项分布似然决定。

[4]:

print("counts has {:d} / {} nonzero elements".format(
    dataset['counts'].count_nonzero(), dataset['counts'].numel()
))

counts has 57129 / 7177464 nonzero elements

为了加快推断（和模型迭代！）速度，我们将用一个等价但便宜得多的 pyro.factor 语句替换 pyro.sample(..., Multinomial) 似然，该语句使用辅助函数 pyro.ops.sparse_multinomial_likelihood。

[5]:

def model(dataset, predict=None):
    features = dataset["features"]
    counts = dataset["counts"]
    sparse_counts = dataset["sparse_counts"]
    assert features.shape[0] == counts.shape[-1]
    S, M = features.shape
    T, P, S = counts.shape
    time = torch.arange(float(T)) * dataset["time_step_days"] / 5.5
    time -= time.mean()

    # Model each region as multivariate logistic growth.
    rate_scale = pyro.sample("rate_scale", dist.LogNormal(-4, 2))
    init_scale = pyro.sample("init_scale", dist.LogNormal(0, 2))
    with pyro.plate("mutation", M, dim=-1):
        coef = pyro.sample("coef", dist.Laplace(0, 0.5))
    with pyro.plate("strain", S, dim=-1):
        rate_loc = pyro.deterministic("rate_loc", 0.01 * coef @ features.T)
        with pyro.plate("place", P, dim=-2):
            rate = pyro.sample("rate", dist.Normal(rate_loc, rate_scale))
            init = pyro.sample("init", dist.Normal(0, init_scale))
    if predict is not None:  # Exit early during evaluation.
        probs = (init + rate * time[predict]).softmax(-1)
        return probs
    logits = (init + rate * time[:, None, None]).log_softmax(-1)

    # Observe sequences via a cheap sparse multinomial likelihood.
    t, p, s = sparse_counts["index"]
    pyro.factor(
        "obs",
        sparse_multinomial_likelihood(
            sparse_counts["total"], logits[t, p, s], sparse_counts["value"]
        )
    )

使用均场推断进行初步检查¶

均场正态推断既廉价又稳健，是初步检查后验点估计的好方法，即使后验不确定性可能窄得不合理。我们建议从 AutoNormal guide 开始，并可能将 init_scale 设置为一个小值，例如 init_scale=0.01 或 init_scale=0.001。

请注意，虽然通过 AutoDelta 进行 MAP 估计比均场 AutoNormal 更便宜、更稳健，但 AutoDelta 依赖于坐标系，并且对重新参数化不具有不变性。根据我们的经验，大多数模型受益于某种程度的重新参数化，因此我们建议使用 AutoNormal 而非 AutoDelta，因为 AutoNormal 对重新参数化不那么敏感（AutoDelta 在某些重新参数化模型中可能产生不正确的结果）。

[6]:

def fit_svi(model, guide, lr=0.01, num_steps=1001, log_every=100, plot=True):
    pyro.clear_param_store()
    pyro.set_rng_seed(20211205)
    if smoke_test:
        num_steps = 2

    # Measure model and guide complexity.
    num_latents = sum(
        site["value"].numel()
        for name, site in poutine.trace(guide).get_trace(dataset).iter_stochastic_nodes()
        if not site["infer"].get("is_auxiliary")
    )
    num_params = sum(p.unconstrained().numel() for p in pyro.get_param_store().values())
    print(f"Found {num_latents} latent variables and {num_params} learnable parameters")

    # Save gradient norms during inference.
    series = defaultdict(list)
    def hook(g, series):
        series.append(torch.linalg.norm(g.reshape(-1), math.inf).item())
    for name, value in pyro.get_param_store().named_parameters():
        value.register_hook(
            functools.partial(hook, series=series[name + " grad"])
        )

    # Train the guide.
    optim = ClippedAdam({"lr": lr, "lrd": 0.1 ** (1 / num_steps)})
    svi = SVI(model, guide, optim, Trace_ELBO())
    num_obs = int(dataset["counts"].count_nonzero())
    for step in range(num_steps):
        loss = svi.step(dataset) / num_obs
        series["loss"].append(loss)
        median = guide.median()  # cheap for autoguides
        for name, value in median.items():
            if value.numel() == 1:
                series[name + " mean"].append(float(value))
        if step % log_every == 0:
            print(f"step {step: >4d} loss = {loss:0.6g}")

    # Plot series to assess convergence.
    if plot:
        plt.figure(figsize=(6, 6))
        for name, Y in series.items():
            if name == "loss":
                plt.plot(Y, "k--", label=name, zorder=0)
            elif name.endswith(" mean"):
                plt.plot(Y, label=name, zorder=-1)
            else:
                plt.plot(Y, label=name, alpha=0.5, lw=1, zorder=-2)
        plt.xlabel("SVI step")
        plt.title("loss, scalar parameters, and gradient norms")
        plt.yscale("log")
        plt.xscale("symlog")
        plt.xlim(0, None)
        plt.legend(loc="best", fontsize=8)
        plt.tight_layout()

[7]:

%%time
guide = AutoNormal(model, init_scale=0.01)
fit_svi(model, guide)

Found 538452 latent variables and 1068600 learnable parameters
step    0 loss = 273.123
step  100 loss = 63.2423
step  200 loss = 44.9539
step  300 loss = 34.8813
step  400 loss = 30.4243
step  500 loss = 27.5258
step  600 loss = 25.4543
step  700 loss = 23.9134
step  800 loss = 22.7201
step  900 loss = 21.8574
step 1000 loss = 21.2031
CPU times: user 3min 4s, sys: 2min 48s, total: 5min 52s
Wall time: 1min 47s

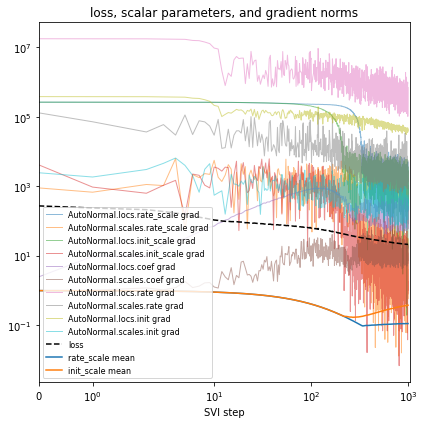
在每次更改模型或推断后，您都将验证模型输出，从而完成 Box 循环。在我们的运行示例中，我们将使用最后一个完全观测时间步长的平均绝对误差 (MAE) 进行定量评估。

[8]:

def mae(true_counts, pred_probs):
    """Computes mean average error between counts and predicted probabilities."""
    pred_counts = pred_probs * true_counts.sum(-1, True)
    error = (true_counts - pred_counts).abs().sum(-1)
    total = true_counts.sum(-1).clamp(min=1)
    return (error / total).mean().item()

def evaluate(
    model, guide, num_particles=100, location="USA / Massachusetts", time=-2
):
    if smoke_test:
        num_particles = 4
    """Evaluate posterior predictive accuracy at the last fully observed time step."""
    with torch.no_grad(), poutine.mask(mask=False):  # makes computations cheaper
        with pyro.plate("particle", num_particles, dim=-3):  # vectorizes
            guide_trace = poutine.trace(guide).get_trace(dataset)
            probs = poutine.replay(model, guide_trace)(dataset, predict=time)
        probs = probs.squeeze().mean(0)  # average over Monte Carlo samples
        true_counts = dataset["counts"][time]
        # Compute global and local KL divergence.
        global_mae = mae(true_counts, probs)
        i = dataset["locations"].index(location)
        local_mae = mae(true_counts[i], probs[i])
    return {"MAE (global)": global_mae, f"MAE ({location})": local_mae}

[9]:

pprint(evaluate(model, guide))

{'MAE (USA / Massachusetts)': 0.26023179292678833,
 'MAE (global)': 0.22586050629615784}

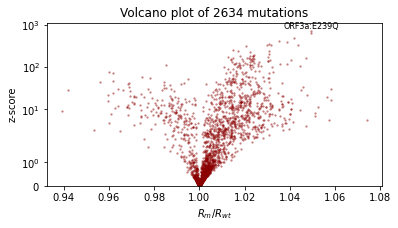
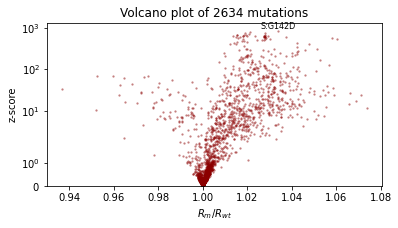
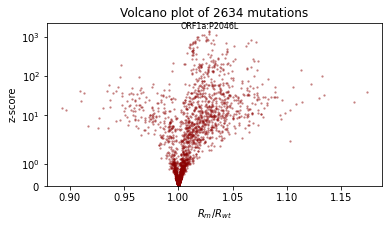
我们还将使用火山图（volcano plot）进行定性评估，火山图显示每个突变系数的效应大小和统计显著性，并标记出具有最显著正效应的突变。我们期望：- 大多数突变影响很小（它们在对数空间中接近零，因此其乘法效应接近 1 倍）- 具有正效应的突变多于负效应的突变 - 效应大小约为 1.1 或 0.9。

[10]:

def plot_volcano(guide, num_particles=100):
    if smoke_test:
        num_particles = 4
    with torch.no_grad(), poutine.mask(mask=False):  # makes computations cheaper
        with pyro.plate("particle", num_particles, dim=-3):  # vectorizes
            trace = poutine.trace(guide).get_trace(dataset)
            trace = poutine.trace(poutine.replay(model, trace)).get_trace(dataset, -1)
            coef = trace.nodes["coef"]["value"].cpu()
    coef = coef.squeeze() * 0.01  # Scale factor as in the model.
    mean = coef.mean(0)
    std = coef.std(0)
    z_score = mean.abs() / std
    effect_size = mean.exp().numpy()
    plt.figure(figsize=(6, 3))
    plt.scatter(effect_size, z_score.numpy(), lw=0, s=5, alpha=0.5, color="darkred")
    plt.yscale("symlog")
    plt.ylim(0, None)
    plt.xlabel("$R_m/R_{wt}$")
    plt.ylabel("z-score")
    i = int((mean / std).max(0).indices)
    plt.text(effect_size[i], z_score[i] * 1.1, dataset["mutations"][i], ha="center", fontsize=8)
    plt.title(f"Volcano plot of {len(mean)} mutations")

plot_volcano(guide)

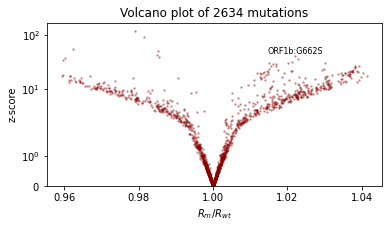
创建初始化启发式方法¶

在高维模型中，即使从弱信息先验中采样，收敛也可能很慢且容易出现 NAN。我们建议启发式地为每个潜变量初始化一个点估计，目标是初始化为一个数量级正确的数值。通常，您可以初始化为数据的简单统计量，例如均值或标准差。

Pyro 的 autoguides 提供了多种初始化策略，用于初始化许多变分族的位置参数，通过 init_loc_fn 指定。您可以通过接受一个 pyro 采样站点字典并使用例如 site["fn"].shape()、site["fn"].support、site["fn"].mean 或通过 site["fn"].sample() 采样从 site["name"] 和 site["fn"] 生成样本来创建自定义初始化器。

[11]:

def init_loc_fn(site):
    shape = site["fn"].shape()
    if site["name"] == "coef":
        return torch.randn(shape).sub_(0.5).mul(0.01)
    if site["name"] == "init":
        # Heuristically initialize based on data.
        return dataset["counts"].mean(0).add(0.01).log()
    return init_to_feasible(site)  # fallback

在您演化模型时，您会添加、移除和重命名潜变量。我们发现要求所有潜变量都有初始化，并在模型更改时添加提示来提醒自己更新 init_loc_fn 是很有用的。

[12]:

def init_loc_fn(site):
    shape = site["fn"].shape()
    if site["name"].endswith("_scale"):
        return torch.ones(shape)
    if site["name"] == "coef":
        return torch.randn(shape).sub_(0.5).mul(0.01)
    if site["name"] == "rate":
        return torch.zeros(shape)
    if site["name"] == "init":
        return dataset["counts"].mean(0).add(0.01).log()
    raise NotImplementedError(f"TODO initialize latent variable {site['name']}")

[13]:

%%time
guide = AutoNormal(model, init_loc_fn=init_loc_fn, init_scale=0.01)
fit_svi(model, guide, lr=0.02)
pprint(evaluate(model, guide))
plot_volcano(guide)

Found 538452 latent variables and 1068600 learnable parameters
step    0 loss = 127.475
step  100 loss = 44.9544
step  200 loss = 31.4236
step  300 loss = 24.4205
step  400 loss = 20.6802
step  500 loss = 18.6063
step  600 loss = 17.2365
step  700 loss = 16.5067
step  800 loss = 16.001
step  900 loss = 15.5123
step 1000 loss = 18.8275
{'MAE (USA / Massachusetts)': 0.29367634654045105,
 'MAE (global)': 0.2283070981502533}
CPU times: user 3min 17s, sys: 2min 51s, total: 6min 9s
Wall time: 1min 58s

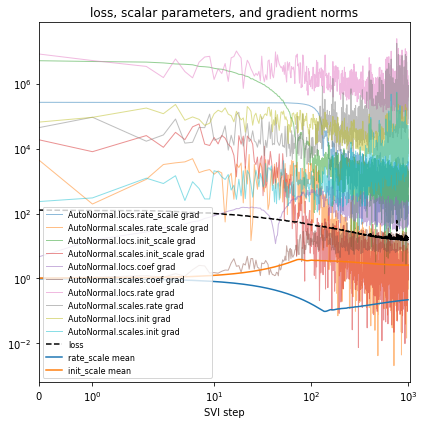
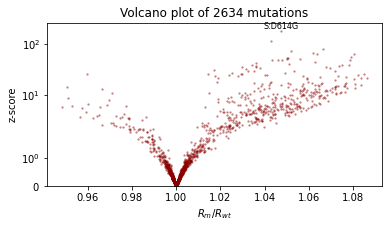
对模型进行重新参数化¶

重新参数化模型可以在改变其几何结构的同时保留其分布。重新参数化本质上是一种坐标变换。重新参数化的目标是扭曲模型的几何结构，以消除相关性，并将不方便的拓扑流形提升到更简单的高维欧氏空间中。

虽然许多概率编程语言要求用户重写模型来改变坐标，但 Pyro 实现了一个包含大约 15 种不同重新参数化效果的库，包括去中心化 (Gorinova et al. 2020)、Haar 小波变换和神经传输 (Hoffman et al. 2019)，以及自动应用效果和创建自定义重新参数化效果的机制。使用这些 reparametrizers，您可以将建模与推断分离：首先以领域专家习惯的形式指定模型，然后在推断代码中，重新参数化模型，使其具有更适合变分推断的几何结构。

在我们的 SARS-CoV-2 模型中，如果我们将

- rate = pyro.sample("rate", dist.Normal(rate_loc, rate_scale))
+ rate = pyro.sample("rate", dist.Normal(0, 1)) * rate_scale + rate_loc

但这会降低模型的可解释性。相反，我们可以重新参数化模型。

[14]:

reparam_model = poutine.reparam(model, config={"rate": LocScaleReparam()})

甚至自动应用一组推荐的 reparameterizers

[15]:

reparam_model = AutoReparam()(model)

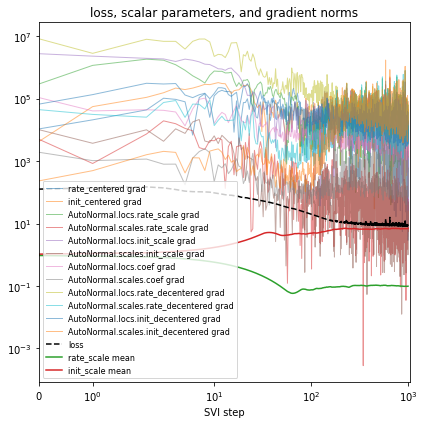
让我们尝试对“rate”和“init”这两个 site 进行重新参数化。请注意，每次训练 guide 时，我们都会创建一个新的 reparam_model，因为参数存储在该 reparam_model 实例中。务必在下游预测任务中使用 reparam_model，例如运行 evaluate(reparam_model, guide)。

[16]:

%%time
reparam_model = poutine.reparam(
    model, {"rate": LocScaleReparam(), "init": LocScaleReparam()}
)
guide = AutoNormal(reparam_model, init_loc_fn=init_loc_fn, init_scale=0.01)
fit_svi(reparam_model, guide, lr=0.05)
pprint(evaluate(reparam_model, guide))
plot_volcano(guide)

Found 538452 latent variables and 1068602 learnable parameters
step    0 loss = 127.368
step  100 loss = 20.2831
step  200 loss = 11.0703
step  300 loss = 9.64594
step  400 loss = 9.52988
step  500 loss = 9.09012
step  600 loss = 9.25454
step  700 loss = 8.60661
step  800 loss = 8.9332
step  900 loss = 8.64206
step 1000 loss = 8.56663
{'MAE (USA / Massachusetts)': 0.1336274892091751,
 'MAE (global)': 0.1719919890165329}
CPU times: user 4min 21s, sys: 3min 9s, total: 7min 31s
Wall time: 2min 17s

定制变分族¶

创建新模型时，我们建议从使用 AutoNormal guide 的均场变分推断开始。这个均场 guide 擅长找到模型众数的邻域，但它天真地忽略了潜变量之间的相关性。捕捉相关性的第一步是如上所述重新参数化模型：使用 LocScaleReparam 或 HaarReparam（在适当的情况下）已经允许 guide 捕捉潜变量之间的一些相关性。

建模不确定性的下一步是通过尝试其他 autoguides、基于EasyGuide 或使用 Pyro 原语创建自定义 guide 来定制变分族。我们建议通过以下步骤逐步增加 guide 的复杂性：1. 从 AutoNormal guide 开始。2. 尝试 AutoLowRankMultivariateNormal，它可以建模相关不确定性的主成分。（对于只有约 100 个潜变量的模型，您也可以尝试 AutoMultivariateNormal 或 AutoGaussian）。3. 尝试使用 AutoGuideList 组合多个 guide。例如，如果 AutoLowRankMultivariateNormal 对所有潜变量来说太昂贵，您可以使用 AutoGuideList 来组合一个针对少量顶层全局潜变量的 AutoLowRankMultivariateNormal guide，以及一个针对更多局部潜变量的更便宜的 AutoNormal guide。4. 尝试使用 AutoGuideList 将 autoguide 与使用 pyro.sample、pyro.param 和 pyro.plate 构建的自定义 guide 函数组合起来。给定一个仅覆盖少量潜变量的 partial_guide() 函数，您可以像添加 autoguides 一样 AutoGuideList.append(partial_guide)。5. 考虑定制 Pyro 中利用模型结构的 autoguides 之一，例如 AutoStructured、AutoNormalMessenger、AutoHierarchicalNormalMessenger AutoRegressiveMessenger。6. 对于具有局部相关性的模型，考虑基于 EasyGuide 进行构建，这是一个用于构建覆盖变量组的 guides 的框架。

虽然完全使用 pyro.sample 原语构建的自定义 guides 提供了最灵活的变分族，但它们也是最脆弱的 guides，因为模型或 reparametrizer 的每次代码更改都需要更改 guide。作者建议避免完全低层次的 guides，而是对模型的至少某些部分使用 AutoGuide 或 EasyGuide，从而加快模型迭代速度。

让我们首先尝试一个简单的 AutoLowRankMultivariateNormal guide。

[17]:

%%time
reparam_model = poutine.reparam(
    model, {"rate": LocScaleReparam(), "init": LocScaleReparam()}
)
guide = AutoLowRankMultivariateNormal(
    reparam_model, init_loc_fn=init_loc_fn, init_scale=0.01, rank=100
)
fit_svi(reparam_model, guide, num_steps=10, log_every=1, plot=False)
# don't even bother to evaluate, since this is too slow.

Found 538452 latent variables and 54498602 learnable parameters
step    0 loss = 128.329
step    1 loss = 126.172
step    2 loss = 124.691
step    3 loss = 123.609
step    4 loss = 123.317
step    5 loss = 121.567
step    6 loss = 120.513
step    7 loss = 121.759
step    8 loss = 120.844
step    9 loss = 121.641
CPU times: user 45.9 s, sys: 38.2 s, total: 1min 24s
Wall time: 29 s

糟糕！这相当慢，有时在 GPU 上会内存不足。

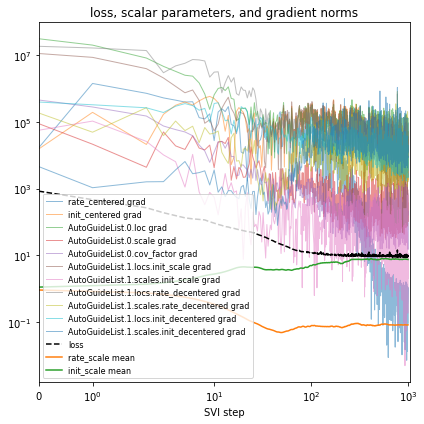
让我们通过使用 AutoGuideList 来降低成本，将一个针对最重要变量 rate_scale、init_scale 和 coef 的 AutoLowRankMultivariateNormal guide 与一个针对模型其余部分（昂贵的 rate 和 init 变量）的简单便宜的 AutoNormal guide 结合起来。典型的模式是使用 poutine.block 创建模型的两个视图，一个暴露目标变量，另一个隐藏它们。

[18]:

%%time
reparam_model = poutine.reparam(
    model, {"rate": LocScaleReparam(), "init": LocScaleReparam()}
)
guide = AutoGuideList(reparam_model)
mvn_vars = ["coef", "rate_scale", "coef_scale"]
guide.add(
    AutoLowRankMultivariateNormal(
        poutine.block(reparam_model, expose=mvn_vars),
        init_loc_fn=init_loc_fn,
        init_scale=0.01,
    )
)
guide.add(
    AutoNormal(
        poutine.block(reparam_model, hide=mvn_vars),
        init_loc_fn=init_loc_fn,
        init_scale=0.01,
    )
)
fit_svi(reparam_model, guide, lr=0.1)
pprint(evaluate(reparam_model, guide))
plot_volcano(guide)

Found 538452 latent variables and 1202987 learnable parameters
step    0 loss = 832.956
step  100 loss = 11.9687
step  200 loss = 11.1152
step  300 loss = 9.60629
step  400 loss = 10.1724
step  500 loss = 9.18063
step  600 loss = 9.1669
step  700 loss = 9.06247
step  800 loss = 9.38853
step  900 loss = 9.12489
step 1000 loss = 8.93582
{'MAE (USA / Massachusetts)': 0.09685955196619034,
 'MAE (global)': 0.16698431968688965}
CPU times: user 4min 22s, sys: 3min 5s, total: 7min 28s
Wall time: 2min 15s

接下来，让我们为模型的一部分创建一个自定义 guide，只针对 rate 和 init 部分。由于我们希望将其与 reparametrizers 一起使用，我们将让 guide 使用 poutine.reparam 创建的辅助潜变量，而不是原始的 rate 和 init 变量。让我们看看这些变量叫什么名字

[19]:

for name, site in poutine.trace(reparam_model).get_trace(
    dataset
).iter_stochastic_nodes():
    print(name)

rate_scale
init_scale
mutation
coef
strain
place
rate_decentered
init_decentered

看起来这些新的辅助变量被称为 rate_decentered 和 init_decentered。

[20]:

def local_guide(dataset):
    # Create learnable parameters.
    T, P, S = dataset["counts"].shape
    r_loc = pyro.param("rate_decentered_loc", lambda: torch.zeros(P, S))
    i_loc = pyro.param("init_decentered_loc", lambda: torch.zeros(P, S))
    skew = pyro.param("skew", lambda: torch.zeros(P, S))  # allows correlation
    r_scale = pyro.param("rate_decentered_scale", lambda: torch.ones(P, S),
                          constraint=constraints.softplus_positive)
    i_scale = pyro.param("init_decentered_scale", lambda: torch.ones(P, S),
                          constraint=constraints.softplus_positive)

    # Sample local variables inside plates.
    # Note plates are already created by the main guide, so we'll
    # use the existing plates rather than calling pyro.plate(...).
    with guide.plates["place"], guide.plates["strain"]:
        samples = {}
        samples["rate_decentered"] = pyro.sample(
            "rate_decentered", dist.Normal(r_loc, r_scale)
        )
        i_loc = i_loc + skew * samples["rate_decentered"]
        samples["init_decentered"] = pyro.sample(
            "init_decentered", dist.Normal(i_loc, i_scale)
        )
    return samples

[21]:

%%time
reparam_model = poutine.reparam(
    model, {"rate": LocScaleReparam(), "init": LocScaleReparam()}
)
guide = AutoGuideList(reparam_model)
local_vars = ["rate_decentered", "init_decentered"]
guide.add(
    AutoLowRankMultivariateNormal(
        poutine.block(reparam_model, hide=local_vars),
        init_loc_fn=init_loc_fn,
        init_scale=0.01,
    )
)
guide.add(local_guide)
fit_svi(reparam_model, guide, lr=0.1)
pprint(evaluate(reparam_model, guide))
plot_volcano(guide)

Found 538452 latent variables and 1468870 learnable parameters
step    0 loss = 4804.42
step  100 loss = 31.7409
step  200 loss = 19.8206
step  300 loss = 15.2961
step  400 loss = 13.2222
step  500 loss = 12.1435
step  600 loss = 11.4291
step  700 loss = 10.9722
step  800 loss = 10.6209
step  900 loss = 10.3649
step 1000 loss = 10.1804
{'MAE (USA / Massachusetts)': 0.1159871369600296,
 'MAE (global)': 0.1876191794872284}
CPU times: user 4min 26s, sys: 3min 7s, total: 7min 33s
Wall time: 2min 18s

结论¶

我们已经了解了如何在贝叶斯工作流程中使用初始化、重新参数化、autoguides 和自定义 guides。有关这些机制的更多示例，我们建议探索 Pyro 代码库，例如在 Pyro 代码库中搜索“poutine.reparam”或“init_loc_fn”。

[ ]: