贝叶斯优化

贝叶斯优化 是一种强大的策略，用于最小化（或最大化）评估成本较高的目标函数。它是 自动化机器学习 工具箱的重要组成部分，例如 auto-sklearn、auto-weka 和 scikit-optimize，在这些工具箱中，贝叶斯优化用于选择模型超参数。贝叶斯优化也用于广泛的其他应用领域；正如文献 [2] 中所列举的，这些领域包括交互式用户界面、机器人学、环境监测、信息提取、组合优化、传感器网络、自适应蒙特卡洛、实验设计和强化学习。

问题设置

我们有一个最小化问题

\[x^* = \text{arg}\min \ f(x),\]

其中 \(f\) 是一个固定的目标函数，我们可以逐点评估。这里我们假设我们没有访问 \(f\) 的梯度。我们也考虑到 \(f\) 的评估可能存在噪声。

为了解决最小化问题，我们将构建一个点序列 \(\{x_n\}\)，使其收敛到 \(x^*\)。由于我们隐含地假设有一个固定的预算（例如 100 次评估），我们不期望找到精确的最小值 \(x^*\)：目标是在给定分配的预算下获得最佳的近似解。

贝叶斯优化策略如下工作

  1. 在目标函数 \(f\) 上设置先验。每次我们在新点 \(x_n\) 评估 \(f\) 时，我们更新对 \(f(x)\) 的模型。这个模型充当替代目标函数，并反映了我们对 \(f\) 的信念（特别是在我们期望 \(f(x)\) 接近 \(f(x^*)\) 的位置）。由于我们是贝叶斯方法，我们的信念被编码在一个后验分布中，这使得我们能够系统地推理模型预测的不确定性。

  2. 使用后验分布推导出一个易于评估和微分的“采集”函数 \(\alpha(x)\)（因此优化 \(\alpha(x)\) 很容易）。与 \(f(x)\) 相反，我们通常会在许多点 \(x\) 评估 \(\alpha(x)\)，因为这样做成本很低。

  3. 重复直到收敛

    • 使用采集函数根据以下公式推导下一个查询点

      \[x_{n+1} = \text{arg}\min \ \alpha(x).\]

    • 评估 \(f(x_{n+1})\) 并更新后验分布。

一个好的采集函数应该利用后验分布中编码的不确定性来鼓励在探索（查询我们对 \(f\) 知之甚少的点）和利用（查询我们有充分理由认为 \(x^*\) 可能所在的区域的点）之间取得平衡。随着迭代过程的进行，我们对 \(f\) 的模型不断演变，采集函数也随之变化。如果我们的模型很好，并且我们选择了合理的采集函数，我们期望采集函数将引导查询点 \(x_n\) 朝着 \(x^*\) 靠近。

在本教程中，我们对 \(f\) 的模型将是高斯过程。特别是我们将看到如何使用 Pyro 中的 高斯过程模块 来实现简单的贝叶斯优化过程。

[1]:

import matplotlib.gridspec as gridspec
import matplotlib.pyplot as plt
import torch
import torch.autograd as autograd
import torch.optim as optim
from torch.distributions import constraints, transform_to

import pyro
import pyro.contrib.gp as gp

assert pyro.__version__.startswith('1.9.1')
pyro.set_rng_seed(1)

定义目标函数

为了演示目的，我们将考虑的目标函数是 Forrester 等人 (2008) 函数

\[f(x) = (6x-2)^2 \sin(12x-4), \quad x\in [0, 1].\]

这个函数既有局部最小值也有全局最小值。全局最小值在 \(x^* = 0.75725\)。

[2]:

def f(x):
    return (6 * x - 2)**2 * torch.sin(12 * x - 4)

我们先来绘制 \(f\) 的图。

[3]:

x = torch.linspace(0, 1, 100)
plt.figure(figsize=(8, 4))
plt.plot(x.numpy(), f(x).numpy())
plt.show()
_images/bo_5_0.png

设置高斯过程先验

高斯过程 因其强大的能力和灵活性而成为函数先验的流行选择。高斯过程的核心是其协方差函数 \(k\)，它控制了输入点对 \((x,x^\prime)\) 之间的 \(f(x)\) 的相似性。在这里，我们将使用高斯过程作为目标函数 \(f\) 的先验。给定输入 \(X\) 和相应的带噪声观测 \(y\)，模型形式如下

\[f\sim\mathrm{MultivariateNormal}(0,k(X,X)),\]
\[y\sim f+\epsilon,\]

其中 \(\epsilon\) 是独立同分布 (i.i.d.) 的高斯噪声，\(k(X,X)\) 是一个协方差矩阵，其元素由每对输入 \((x,x^\prime)\) 的 \(k(x,x^\prime)\) 给出。

我们选择 Matern 核，其中 \(\nu = \frac{5}{2}\)（如参考文献 [1] 所示）。请注意，在许多回归任务中使用的流行 RBF 核会产生一个函数先验，其样本是无限可微的；这对于大多数“黑盒”目标函数来说可能是一个不现实的假设。

[4]:

# initialize the model with four input points: 0.0, 0.33, 0.66, 1.0
X = torch.tensor([0.0, 0.33, 0.66, 1.0])
y = f(X)
gpmodel = gp.models.GPRegression(X, y, gp.kernels.Matern52(input_dim=1),
                                 noise=torch.tensor(0.1), jitter=1.0e-4)

下面的辅助函数 update_posterior 将负责每次我们在新的值 \(x\) 评估 \(f\) 时更新我们的 gpmodel。

[5]:

def update_posterior(x_new):
    y = f(x_new) # evaluate f at new point.
    X = torch.cat([gpmodel.X, x_new]) # incorporate new evaluation
    y = torch.cat([gpmodel.y, y])
    gpmodel.set_data(X, y)
    # optimize the GP hyperparameters using Adam with lr=0.001
    optimizer = torch.optim.Adam(gpmodel.parameters(), lr=0.001)
    gp.util.train(gpmodel, optimizer)

定义采集函数

对于采集函数有很多合理的选择（参见参考文献 [1] 和 [2] 了解常用选择及其属性的讨论）。这里我们将使用一个“简单易于实现和解释”的采集函数，即“下置信界”（Lower Confidence Bound）采集函数。其定义为

\[\alpha(x) = \mu(x) - \kappa \sigma(x)\]

其中 \(\mu(x)\) 和 \(\sigma(x)\) 分别是在点 \(x\) 的后验均值和方差的平方根，任意常数 \(\kappa>0\) 控制着利用和探索之间的权衡。这个采集函数将在以下情况下最小化 \(x\) 的选择：i) \(\mu(x)\) 较小（利用）；或 ii) \(\sigma(x)\) 较大（探索）。较大的 \(\kappa\) 值意味着我们更注重探索，因为我们偏好在高不确定性区域中的候选点 \(x\)。较小的 \(\kappa\) 值鼓励利用，因为我们偏好最小化 \(\mu(x)\) 的候选点 \(x\)，这是我们替代目标函数的均值。我们将使用 \(\kappa=2\)。

[6]:

def lower_confidence_bound(x, kappa=2):
    mu, variance = gpmodel(x, full_cov=False, noiseless=False)
    sigma = variance.sqrt()
    return mu - kappa * sigma

我们需要的最后一个组件是找到采集函数的（近似）最小化点 \(x_{\rm min}\) 的方法。有几种方法可以进行，包括基于梯度和非基于梯度的技术。这里我们将采用基于梯度的方法。梯度下降方法的一个可能缺点是最小化算法可能会陷入局部最小值。在本教程中，我们采用一种（非常）简单的方法来解决这个问题

  • 首先，我们用 5 个不同的值作为最小化算法的种子：i) 其中一个选择为 \(x_{n-1}\)，即前一步使用的候选点 \(x\)；ii) 另外四个从目标函数的定义域中均匀随机选择。

  • 然后，对每个种子值运行最小化算法，直到近似收敛。

  • 最后，从最小化算法确定的五个候选点 \(x\) 中，我们选择最小化采集函数的那个点。

有关贝叶斯优化中此问题的更详细讨论，请参阅参考文献 [2]。

[7]:

def find_a_candidate(x_init, lower_bound=0, upper_bound=1):
    # transform x to an unconstrained domain
    constraint = constraints.interval(lower_bound, upper_bound)
    unconstrained_x_init = transform_to(constraint).inv(x_init)
    unconstrained_x = unconstrained_x_init.clone().detach().requires_grad_(True)
    minimizer = optim.LBFGS([unconstrained_x], line_search_fn='strong_wolfe')

    def closure():
        minimizer.zero_grad()
        x = transform_to(constraint)(unconstrained_x)
        y = lower_confidence_bound(x)
        autograd.backward(unconstrained_x, autograd.grad(y, unconstrained_x))
        return y

    minimizer.step(closure)
    # after finding a candidate in the unconstrained domain,
    # convert it back to original domain.
    x = transform_to(constraint)(unconstrained_x)
    return x.detach()

贝叶斯优化的内循环

利用上面定义的各种辅助函数，我们现在可以将贝叶斯优化单一步骤的主要逻辑封装在函数 next_x 中

[8]:

def next_x(lower_bound=0, upper_bound=1, num_candidates=5):
    candidates = []
    values = []

    x_init = gpmodel.X[-1:]
    for i in range(num_candidates):
        x = find_a_candidate(x_init, lower_bound, upper_bound)
        y = lower_confidence_bound(x)
        candidates.append(x)
        values.append(y)
        x_init = x.new_empty(1).uniform_(lower_bound, upper_bound)

    argmin = torch.min(torch.cat(values), dim=0)[1].item()
    return candidates[argmin]

运行算法

为了说明贝叶斯优化如何工作，我们创建一个方便的绘图函数，它将帮助我们可视化算法的进展。

[9]:

def plot(gs, xmin, xlabel=None, with_title=True):
    xlabel = "xmin" if xlabel is None else "x{}".format(xlabel)
    Xnew = torch.linspace(-0.1, 1.1, 100)
    ax1 = plt.subplot(gs[0])
    ax1.plot(gpmodel.X.numpy(), gpmodel.y.numpy(), "kx")  # plot all observed data
    with torch.no_grad():
        loc, var = gpmodel(Xnew, full_cov=False, noiseless=False)
        sd = var.sqrt()
        ax1.plot(Xnew.numpy(), loc.numpy(), "r", lw=2)  # plot predictive mean
        ax1.fill_between(Xnew.numpy(), loc.numpy() - 2*sd.numpy(), loc.numpy() + 2*sd.numpy(),
                         color="C0", alpha=0.3)  # plot uncertainty intervals
    ax1.set_xlim(-0.1, 1.1)
    ax1.set_title("Find {}".format(xlabel))
    if with_title:
        ax1.set_ylabel("Gaussian Process Regression")

    ax2 = plt.subplot(gs[1])
    with torch.no_grad():
        # plot the acquisition function
        ax2.plot(Xnew.numpy(), lower_confidence_bound(Xnew).numpy())
        # plot the new candidate point
        ax2.plot(xmin.numpy(), lower_confidence_bound(xmin).numpy(), "^", markersize=10,
                 label="{} = {:.5f}".format(xlabel, xmin.item()))
    ax2.set_xlim(-0.1, 1.1)
    if with_title:
        ax2.set_ylabel("Acquisition Function")
    ax2.legend(loc=1)

我们的替代模型 gpmodel 已经进行了 4 次函数评估；但是，我们还没有优化 GP 超参数。所以我们首先进行优化。然后在一个循环中，我们重复调用 next_x 和 update_posterior 函数。下面的图示说明了高斯过程后验分布和相应的采集函数在算法的每个步骤中如何变化。注意查询点是如何同时为了探索和利用而选择的。

[10]:

plt.figure(figsize=(12, 30))
outer_gs = gridspec.GridSpec(5, 2)
optimizer = torch.optim.Adam(gpmodel.parameters(), lr=0.001)
gp.util.train(gpmodel, optimizer)
for i in range(8):
    xmin = next_x()
    gs = gridspec.GridSpecFromSubplotSpec(2, 1, subplot_spec=outer_gs[i])
    plot(gs, xmin, xlabel=i+1, with_title=(i % 2 == 0))
    update_posterior(xmin)
plt.show()
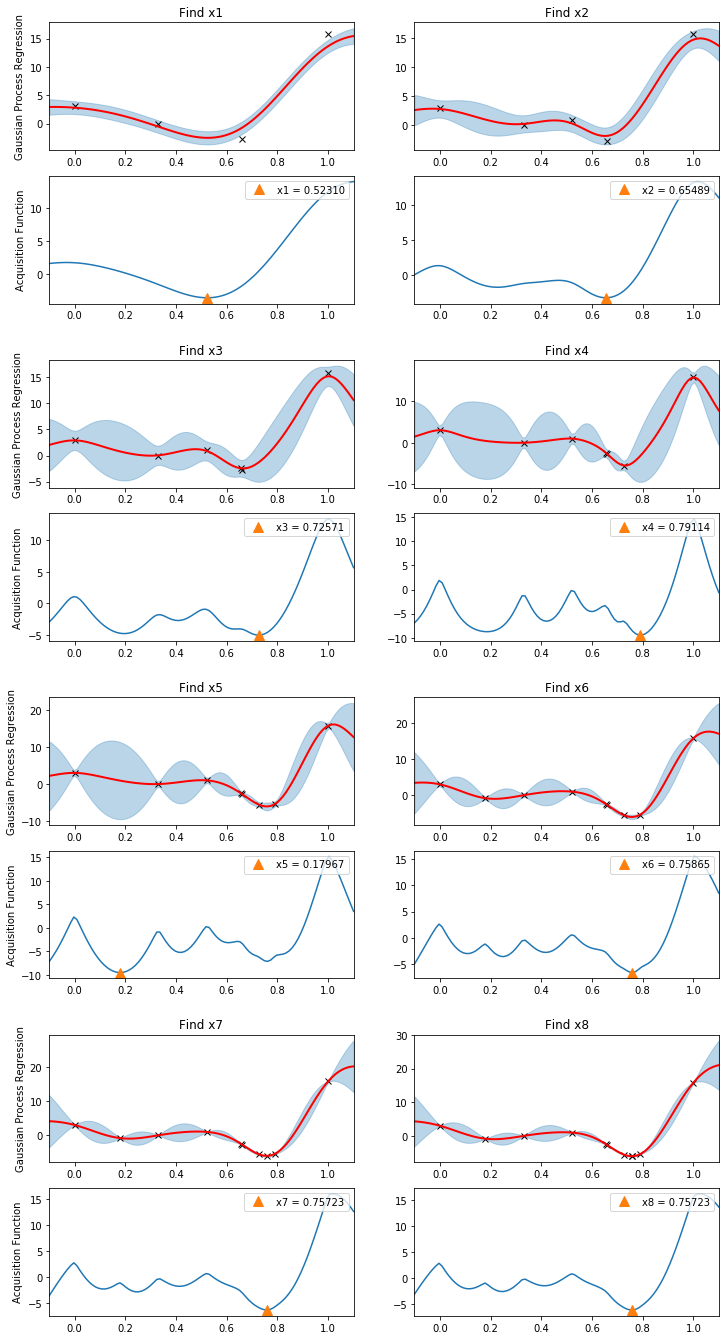
_images/bo_22_0.png

由于我们假设观测数据包含噪声，因此我们不太可能找到函数 \(f\) 的精确最小化点。尽管如此，在相对较小的评估预算（8 次）下，我们看到算法已经收敛到非常接近全局最小值 \(x^* = 0.75725\) 的位置。

虽然本教程仅旨在简要介绍贝叶斯优化，但我们希望能够传达其基本思想。考虑观看 Nando de Freitas [3] 的讲座，他对基本理论进行了精彩的阐述。最后，参考文献 [2] 回顾了最近关于贝叶斯优化的研究，并讨论了许多重要的技术细节。

参考文献

[1] 机器学习算法的实用贝叶斯优化,     Jasper Snoek, Hugo Larochelle, and Ryan P. Adams

[2] 将人类排除在循环之外：贝叶斯优化综述,     Bobak Shahriari, Kevin Swersky, Ziyu Wang, Ryan P. Adams, and Nando De Freitas

[3] 机器学习 - 贝叶斯优化和多臂老虎机